题目内容
圆锥体的高是3cm,它的侧面展开图是一个半圆,这个圆锥的侧面积是( )
| A、6πcm2 |
| B、8πcm2 |
| C、9πcm2 |
| D、12πcm2 |
考点:圆锥的计算
专题:
分析:设圆锥的底面半径为r,母线长为l,用两种方式表示出侧面积,即可求得圆锥底面半径r和母线长l的关系,加上高利用勾股定理即可求得l和r,那么圆锥的侧面积=πrl,代入数据计算即可求解.
解答:解:设底面半径为r,母线长为l,则底面周长=2πr,
∵侧面积=
×2πrl=
πl2,
∴l=2r,
由勾股定理得,l2=(
l)2+32,
∴l=2
,r=
,
∴圆锥的侧面积=πrl=π×
×2
=6π(cm2).
故选A.
∵侧面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴l=2r,
由勾股定理得,l2=(
| 1 |
| 2 |
∴l=2
| 3 |
| 3 |
∴圆锥的侧面积=πrl=π×
| 3 |
| 3 |
故选A.
点评:本题考查了圆锥的计算,利用了勾股定理,圆的面积公式,圆锥的侧面积计算公式,理解圆锥的母线长是侧面展开图中扇形的半径是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
在+(-6),-(-3),-8,-22,-|-4|中,负数共有( )
| A、5个 | B、4个 | C、3个 | D、2个 |
有6个大小、质地完全一样的球,2个红球,4个白球,装在盒子里搅匀,从中先后摸岀两个,摸岀后不放回.摸出的恰好是1个红球1个白球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,点E在AD的延长线上,下列条件能判断AB∥DC的是( )
如图,点E在AD的延长线上,下列条件能判断AB∥DC的是( )| A、∠1=∠2 |
| B、∠3=∠4 |
| C、∠C=∠CDE |
| D、∠C+∠ADC=180° |
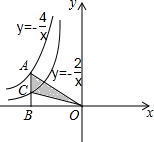 已知,如图,点A在反比例函数y=-
已知,如图,点A在反比例函数y=-