题目内容
8.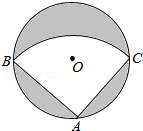 如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )| A. | $\frac{{\sqrt{2}}}{2}$米 | B. | $\frac{{\sqrt{2}}}{4}$米 | C. | $\frac{1}{2}$米 | D. | $\frac{1}{4}$米 |
分析 先利用△ABC为等腰直角三角形得到AB=1,再设圆锥的底面圆的半径为r,则根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=$\frac{90•π•1}{180}$,然后解方程即可.
解答 解:∵⊙O的直径BC=$\sqrt{2}$,
∴AB=$\frac{\sqrt{2}}{2}$BC=1,
设圆锥的底面圆的半径为r,
则2πr=$\frac{90•π•1}{180}$,解得r=$\frac{1}{4}$,
即圆锥的底面圆的半径为$\frac{1}{4}$米.
故选D.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
3.下列各数中,最小的是( )
| A. | 0 | B. | -$\frac{1}{2}$ | C. | 2 | D. | -3 |
13.一组数据1,3,2,0,3,0,2的中位数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
18.下列各数中,最小的是( )
| A. | -2 | B. | 1 | C. | 0 | D. | $\sqrt{3}$ |