题目内容
14.方程x2+5x+6=0的根为x1=-2,x2=-3,二次函数y=x2+5x+6与x轴的交点是(-3,0)与(-2,0).分析 先利用因式分解法解方程得到x1=-2,x2=-3,然后利用抛物线与x轴的交点问题写出抛物线与x轴的交点坐标.
解答 解:x2+5x+6=0,
(x+2)(x+3)=0,
所以x1=-2,x2=-3,
所以二次函数y=x2+5x+6与x轴的交点坐标为(-3,0)和(-2,0).
故答案为x1=-2,x2=-3,(-3,0),(-2,0).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程问题.

练习册系列答案
相关题目
2.国旗是一个国家的象征,下面四个国家的国旗不是轴对称图形的是( )
| A. |  越南 | B. |  澳大利亚 | C. |  加拿大 | D. |  柬埔寨 |
6.化简:$\sqrt{(1-tan60°)^2}$=( )
| A. | 1-$\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$-1 | C. | $\frac{\sqrt{3}}{3}$-1 | D. | 1-$\sqrt{3}$ |
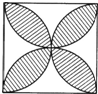 如图所示是一个美丽的图案,它是由一个边长为1的正方形和四个半圆组成的.半圆的直径与正方形的边长相等.它也可以看作是由四个“花瓣”与四个“
如图所示是一个美丽的图案,它是由一个边长为1的正方形和四个半圆组成的.半圆的直径与正方形的边长相等.它也可以看作是由四个“花瓣”与四个“ ”,(空白处)组成的.
”,(空白处)组成的. ”的面积为x.每个“花瓣”的面积为y.试写出x和y之间的两个关系式;
”的面积为x.每个“花瓣”的面积为y.试写出x和y之间的两个关系式; 如图所示,在直角坐标系中,A(-3,1),B(-4,0),C(0,3),D(2,2),E(3,-3),F(-2,-2),作出点A,B,C,D,E,F关于原点O的对称点,写出它们的坐标.并回答:这些坐标与已知的坐标有什么关系?
如图所示,在直角坐标系中,A(-3,1),B(-4,0),C(0,3),D(2,2),E(3,-3),F(-2,-2),作出点A,B,C,D,E,F关于原点O的对称点,写出它们的坐标.并回答:这些坐标与已知的坐标有什么关系?