题目内容
19.观察下面一列数:$\frac{1}{2}$,-$\frac{3}{6}$,$\frac{5}{12}$,-$\frac{7}{20}$,…按照这个规律,第6个数应该是-$\frac{11}{42}$.分析 根据已知4个数得出第n个数为(-1)n+1•$\frac{2n-1}{n(n+1)}$,将n=6代入即可得.
解答 解:∵第1个数$\frac{1}{2}$=(-1)2×$\frac{1}{1×2}$,
第2个数-$\frac{3}{6}$=(-1)2+1×$\frac{2×2-1}{2×3}$,
第3个数$\frac{5}{12}$=(-1)3+1×$\frac{2×3-1}{3×4}$,
…
∴第n个数为(-1)n+1•$\frac{2n-1}{n(n+1)}$,
当n=6时,(-1)n+1•$\frac{2n-1}{n(n+1)}$=-$\frac{11}{42}$,
故答案为:-$\frac{11}{42}$.
点评 本题考查了数字的变化类题目,解题的关键是根据题目的变化规律得到相应的结果.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
7.正五边形的每个内角都等于( )
| A. | 60° | B. | 90° | C. | 108° | D. | 120° |
8.下列各式中计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | 3+$\sqrt{2}$=3$\sqrt{2}$ | C. | m$\sqrt{b}$-n$\sqrt{b}$=(m-n)$\sqrt{b}$ | D. | $\frac{\sqrt{50}-\sqrt{32}}{2}$=$\sqrt{25}$-$\sqrt{16}$=1 |
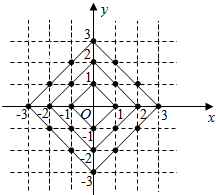 在平面直角坐标系中,横坐标、纵坐标都是整数的点称为整点,观察图中 每一个正方形(实线)四条边上的整点的个数,请你猜测出里向外第2016个正方形(实线)四条边上的整点个数共有8064个.
在平面直角坐标系中,横坐标、纵坐标都是整数的点称为整点,观察图中 每一个正方形(实线)四条边上的整点的个数,请你猜测出里向外第2016个正方形(实线)四条边上的整点个数共有8064个.