题目内容
1. 用长为20米的篱笆,一面靠墙(墙的长度是8米),围成一个长方形花圃,如图,设AB边的长为x米,花圃的面积为y平方米,则当x=6m时,y最大=
用长为20米的篱笆,一面靠墙(墙的长度是8米),围成一个长方形花圃,如图,设AB边的长为x米,花圃的面积为y平方米,则当x=6m时,y最大=48m2.
分析 由于靠墙的一边不需要篱笆,即篱笆只用做三方,AB=x,则BC=20-2x,用矩形面积公式可表示函数式;但0<BC≤8,于是得到结论.
解答 解:根据已知得,AB=x,则BC=20-2x,
所以,矩形面积y=x(20-2x),
即y=-2x2+20x=-2(x-5)2+50,
∵a=-2<0,当x<5时,y随x的增大,
∵墙的长度是8米,
∴当x=6时,y最大=48m2.
故答案为:6m,48m2.
点评 本题考查了矩形的面积公式的运用,二次函数的解析式的运用,由函数值求自变量的值的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
13.已知点(-6,y1),(3,y2)都在直线y=-$\frac{1}{3}$x+5 上,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
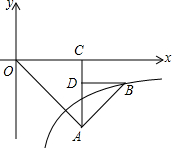 如图,△OAC和△BAD都是等腰直角三角形,反比例函数在第四象限经过点B,若OA2-AB2=8,则k的值为-4.
如图,△OAC和△BAD都是等腰直角三角形,反比例函数在第四象限经过点B,若OA2-AB2=8,则k的值为-4.