Question

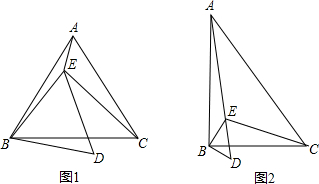
9．已知点E在△ABC内，∠ABC=∠EBD=α，∠ACB=∠EDB=60°，∠AEB=150°，∠BEC=90°．
（1）如图1，当α=60°时，△ABC是等边三角形；
（2）在（1）的条件下，连接CD．
①求证：△BAE≌△BCD；②若AE=1，试求BD的长；
（3）如图2，当α=90°时，直接写出$\frac{BD}{AE}$的值．

Answer 1

分析 （1）由三角形ABC中有两个60°的角，即可求得它为等边三角形；
（2）①由△EBD也是等边三角形，连接DC，证得△ABE≌△CBD，②根据全等三角形的性质得到AE=CD，∠AEB=∠CDB=150°在直角三角形中很容易证得结论；
（3）连接DC，证得△ABC∽△EBD，设BD=x在Rt△EBD中DE=2x由相似比即得到比值．

解答 解：（1）△ABC是等边三角形，
理由：∵∠ABC=∠ACB=60°
∴∠BAC=180°-∠ABC-∠ACB=60°=∠ABC=∠ACB
∴△ABC是等边三角形；
故答案为：等边；

（2）①证明：连接DC，
∵∠ABC=∠ACB=60°，
∴∠BAC=180°-∠ABC-∠ACB=60°=∠ABC=∠ACB，
∴△ABC是等边三角形，
同理△EBD也是等边三角形，
∴AB=BC，BE=BD，∠ABE=60°-∠EBC=∠CBD，
在△ABE与△CBD中，
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBD}\\{BE=BD}\end{array}\right.$，
∴△ABE≌△CBD；
②∵△ABE≌△CBD，
∴AE=CD，∠AEB=∠CDB=150°
∴∠EDC=150°-∠BDE=90°∠CED=∠BEC-∠BED=90°-60°=30°．
在Rt△EDC中，$\frac{CD}{ED}=tan30°=\frac{\sqrt{3}}{3}$，∴$\frac{AE}{BD}=\frac{\sqrt{3}}{3}$，∴BD=$\sqrt{3}$AE； 

（3）如图2，连接DC，
∵∠ABC=∠EBD=90°，∠ACB=∠EDB=60°
∴△ABC∽△EBD，
∴$\frac{AB}{EB}$=$\frac{BC}{BD}$，即$\frac{AB}{BC}=\frac{EB}{BD}$，
又∵∠ABE=90°-∠EBC=∠CBD，
∴△ABE∽△CBD，∠AEB=∠CDB=150°，
∴$\frac{AE}{CD}$=$\frac{BE}{BD}$，
∴∠EDC=150°-∠BDE=90°，∠CED=∠BEC-∠BED=90°-（90°-∠BDE）=60°，
设BD=x，在Rt△EBD中DE=2x，BE=$\sqrt{3}$x，
在Rt△EDC中CD=DE•tan60°=2$\sqrt{3}$x，
∴AE=$\frac{CD•BE}{BD}$=$\frac{2×\sqrt{3}x•\sqrt{3}x}{x}$=6x=6BD，
即$\frac{BD}{AE}$=$\frac{1}{6}$．

点评 本题考查了相似三角形的判定和性质，全等三角形的判定和性质，等边三角形的判定和性质，解直角三角形，证得△ABE∽△CBD是解题的关键．