题目内容
9.已知直线y=-x+6和y=x-2,则它们与y轴所围成的三角形的面积为( )| A. | 6 | B. | 10 | C. | 16 | D. | 12 |
分析 首先求得两直线的交点坐标,然后求得两函数图象与y轴的交点坐标,然后求得与y轴围成的三角形的面积即可.
解答 解:联立$\left\{\begin{array}{l}{y=-x+6}\\{y=x-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,
所以,两直线的交点坐标为(4,2),
令x=0,则y=6,y=-2,
所以,两直线与y轴的交点坐标分别为(0,6),(0,-2),
∴它们与y轴所围成的三角形的面积$\frac{1}{2}×(6+2)×4=16$,
故选C.
点评 本题考查了两直线相交的问题,三角形的面积,联立两直线解析式求交点坐标是常用的方法,需熟练掌握并灵活运用.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
17. 如图,下列表示角的方法,错误的是( )
如图,下列表示角的方法,错误的是( )
 如图,下列表示角的方法,错误的是( )
如图,下列表示角的方法,错误的是( )| A. | ∠1与∠AOB表示同一个角 | B. | ∠AOC也可用∠O来表示 | ||
| C. | 图中共有三个角:∠AOB、∠AOC、∠BOC | D. | ∠β表示的是∠BOC |
14.四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:
①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AB∥CD,AD=BC;④AO=CO,BO=DO.
其中一定能判定这个四边形是平行四边形的条件有( )
①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AB∥CD,AD=BC;④AO=CO,BO=DO.
其中一定能判定这个四边形是平行四边形的条件有( )
| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
18.学校到县城有28千米,全程需1小时,除乘汽车外,还需要步行一段路,已知汽车的速度为36千米/时,人步行的速度为4千米/时,则步行用了( )
| A. | 13分钟 | B. | 14分钟 | C. | 15分钟 | D. | 16分钟 |
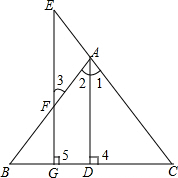 已知:如图,AD⊥BC于D,EG⊥BC于G,AD是∠BAC的角平分线,试说明∠E=∠3.
已知:如图,AD⊥BC于D,EG⊥BC于G,AD是∠BAC的角平分线,试说明∠E=∠3. 如图所示,AB∥CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=1,则AB与CD之间的距离等于2.
如图所示,AB∥CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=1,则AB与CD之间的距离等于2. 已知:如图,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b(a≠0)的图象交于A(3,1)、B(m,-3)两点.
已知:如图,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b(a≠0)的图象交于A(3,1)、B(m,-3)两点.