题目内容
19. 已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.
已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.
分析 先由AAS证明△ADC≌△AEB,得出AD=AE,再由HL证明Rt△AOD≌Rt△AOE,得出∠OAD=∠OAE,即可得出结论.
解答 证明:∵CD⊥AB于D,BE⊥AC于E,
∴∠ADC=∠AEB=90°,
在△ADC和△AEB中,$\left\{\begin{array}{l}{∠ADC=∠AEB}&{\;}\\{∠DAC=∠EAB}&{\;}\\{AC=AB}&{\;}\end{array}\right.$,
∴△ADC≌△AEB(AAS),
∴AD=AE,
在Rt△AOD和Rt△AOE中,$\left\{\begin{array}{l}{OA=OA}&{\;}\\{AD=AE}&{\;}\end{array}\right.$,
∴Rt△AOD≌Rt△AOE(HL),
∴∠OAD=∠OAE,
∴AO平分∠BAC.
点评 本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.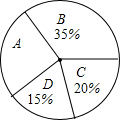 某中学九年级1班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示,
某中学九年级1班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示,
其中评价为“A”所在扇形的圆心角是( )
 某中学九年级1班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示,
某中学九年级1班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示,其中评价为“A”所在扇形的圆心角是( )
| A. | 120° | B. | 108° | C. | 90° | D. | 30° |
8.若二次根式$\sqrt{2x-1}$有意义,则x的取值范围是( )
| A. | x≤-$\frac{1}{2}$ | B. | x≥-$\frac{1}{2}$ | C. | x≥$\frac{1}{2}$ | D. | x≤$\frac{1}{2}$ |
9.正六边形的每一个外角都是( )
| A. | 720° | B. | 360° | C. | 120° | D. | 60° |
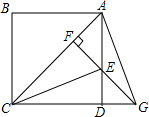 如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.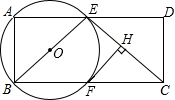 已知矩形ABCD中,AB=2,AD=5,点E是AD边上一动点,连接BE,CE,以BE为直径作⊙O,交BC于点F,过点F作FH⊥CE于点H,直线FH交⊙O于点G.
已知矩形ABCD中,AB=2,AD=5,点E是AD边上一动点,连接BE,CE,以BE为直径作⊙O,交BC于点F,过点F作FH⊥CE于点H,直线FH交⊙O于点G.