题目内容
7.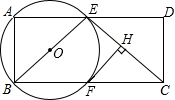 已知矩形ABCD中,AB=2,AD=5,点E是AD边上一动点,连接BE,CE,以BE为直径作⊙O,交BC于点F,过点F作FH⊥CE于点H,直线FH交⊙O于点G.
已知矩形ABCD中,AB=2,AD=5,点E是AD边上一动点,连接BE,CE,以BE为直径作⊙O,交BC于点F,过点F作FH⊥CE于点H,直线FH交⊙O于点G.(1)当直线FH与⊙O相切时,求AE的长;
(2)当FH∥BE时,求FG的长.
分析 (1)连接EF,FA,由CE为圆的切线且又和EB垂直,可知CE∥FA,推出∠CEF=∠AFE,而∠AFE=∠FEB可得∠CEF=∠BEF,所以EF为∠BEC的平分线.又因为∠EFB为直角可知EF⊥BC,所以△BEC为等腰三角形,得到BF为BC的一半,又因为EA∥CF,可知四边形CEAF为平行四边形,即AD=BF=2.5;
(2)作OM⊥FG于点M,连接OF,先证明△ABE∽△CDE,得出$\frac{AE}{CD}$,求出AE=1或AE=4;①当AE=1时,证明△CFH∽△CBE,得出比例式$\frac{CH}{CE}$,求出CH、OM,根据勾股定理求出FM,即可得出FG=2FM=$\frac{3\sqrt{5}}{5}$;②当AE=4时,同①得出△CFH∽△CBE,得出$\frac{CH}{CE}$,求出CH=$\frac{\sqrt{5}}{5}$,得出OM,由勾股定理求出FM,即可得出FG.
解答 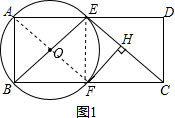 解:(1)如图1,连接EF,FA,
解:(1)如图1,连接EF,FA,
∵CE为圆的切线且又和EB垂直,
∴CE∥AF
∴∠CEF=∠AFE;
又∵∠AFE=∠FEB,
∴∠CEF=∠BEF,
∴EF为∠BEC的平分线;
∵∠EFB=90°,
∴EF⊥BC,
∴BE=CE
∴△BEC为等腰三角形,
∴BF为BC的一半;
∵EA∥CF,
∴四边形CEAF为平行四边形,
即EA=CF=2.5;
(2)解:如图2,作OM⊥FG于点M,连接OF,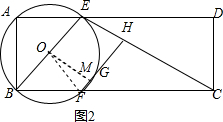
∵FH∥BE,
∴∠BEC=∠FHC=90°,
∠HFC=∠EBF,
又∵∠HFC+∠FCH=90°,∠EBF+∠ABE=90°,
∴∠ABE=∠FCH,
∵∠ABE+∠AEB=90°,∠FCH+∠DCE=90°,
∴∠AEB=∠DCE,
∴△ABE∽△CDE,
∴$\frac{AE}{CD}$,
∴$\frac{AE}{2}$,
解得:AE=1或AE=4;
①当AE=1时,BF=1,DE=CF=4,
∴BE=$\sqrt{5}$,CE=2$\sqrt{5}$,OF=$\frac{\sqrt{5}}{2}$,
∵四边形ABCD是矩形,
∴BC=AD=5,
∵FH∥BE,
∴△CFH∽△CBE,
∴$\frac{CH}{CE}$,即$\frac{CH}{2\sqrt{5}}$,
∴CH=$\frac{8\sqrt{5}}{5}$,
∴OM=EH=CE-CH=$\frac{2\sqrt{5}}{5}$,
∴FM=$\sqrt{{OF}^{2}{-OM}^{2}}$=$\frac{3\sqrt{5}}{10}$,
∴FG=2FM=$\frac{3\sqrt{5}}{5}$;
②当AE=4时,BF=4,DE=CF=1,
∴BE=2$\sqrt{5}$,CE=$\sqrt{5}$,OG=$\sqrt{5}$,
∵△CFH∽△CBE,
∴$\frac{CH}{CE}$,即$\frac{CH}{\sqrt{5}}$,
∴CH=$\frac{\sqrt{5}}{5}$,
∴OM=EH=CE-CH=$\frac{4\sqrt{5}}{5}$,
∴FM=$\sqrt{{OG}^{2}{-OM}^{2}}$=$\frac{3\sqrt{5}}{5}$,
∴FG=2FM=$\frac{6\sqrt{5}}{5}$;
综上所述:FG的长为:$\frac{3\sqrt{5}}{5}$或$\frac{6\sqrt{5}}{5}$;
点评 本题考查了圆周角定理、勾股定理、相似三角形的判定与性质、矩形的性质、等腰直角三角形的判定与性质、切线的判定等知识;本题难度较大,综合性强,特别是(2)中,需要进行分类讨论和证明三角形相似才能得出结果.

 名校课堂系列答案
名校课堂系列答案| A. | 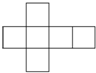 | B. | 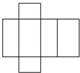 | C. | 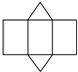 | D. |  |
| A. | 2℃ | B. | -2℃ | C. | 2 | D. | -2 |
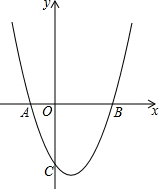 如图,抛物线y=x2-2x+k与x轴交于A,B两点,与y轴交于C(0,-3).
如图,抛物线y=x2-2x+k与x轴交于A,B两点,与y轴交于C(0,-3).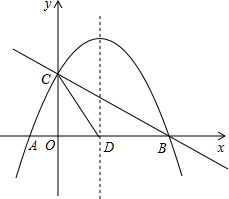 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).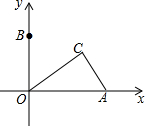 如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.
如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°. 已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.
已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.