题目内容
19. 如图,正方形ABCD中,点E、F分别在AB、AD上,且,∠BCE=∠DCF.求证:AE=AF.
如图,正方形ABCD中,点E、F分别在AB、AD上,且,∠BCE=∠DCF.求证:AE=AF.
分析 由正方形的性质得出AB=BC=DC=AD,∠B=∠D=90°,由ASA证明△BCE≌△DCF,得出对应边相等BE=DF,即可得出AE=AF.
解答 证明:∵四边形ABCD为正方形,
∴AB=BC=DC=AD,∠B=∠D=90°,
在△BCE和△DCF中,
$\left\{\begin{array}{l}{∠BCE=∠DCF}&{\;}\\{BC=DC}&{\;}\\{∠B=∠D}&{\;}\end{array}\right.$,
∴△BCE≌△DCF(ASA),
∴BE=DF,
∴AE=AF.
点评 本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
7.已知:a-3b=2,则6-2a+6b的值为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转15°.
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转15°. 已知:如图,点B(3,3)在双曲线y=$\frac{k}{x}$(其中x>0)上,点D在双曲线y=$\frac{-4}{x}$ (其中x<0)上,点A、C分别在x、y轴的正半轴上,且点A、B、C、D围成的四边形为正方形.
已知:如图,点B(3,3)在双曲线y=$\frac{k}{x}$(其中x>0)上,点D在双曲线y=$\frac{-4}{x}$ (其中x<0)上,点A、C分别在x、y轴的正半轴上,且点A、B、C、D围成的四边形为正方形.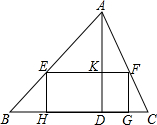 已知锐角△ABC中,边BC长为12,高AD长为8.
已知锐角△ABC中,边BC长为12,高AD长为8.