题目内容
17. 如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,判断线段BF和AC的数量关系和位置关系,并说明理由.
如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,判断线段BF和AC的数量关系和位置关系,并说明理由.
分析 BF⊥AC且BF=AC,因为AD为△ABC上的高,所以∠ADB=∠ADC=90°,又因为BF=AC,FD=CD,则可根据HL判定△ADC≌△BDF进而可得BF=AC,
因为∠EBC=∠DAC,又因为∠DAC+∠ACD=90°,所以∠EBC+∠ACD=90°,则BE⊥AC即BF⊥AC.
解答 解:BF⊥AC且BF=AC,
理由如下:
证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△ADC和△BDF中
$\left\{\begin{array}{l}{BF=AC}\\{FD=CD}\end{array}\right.$,
∴△ADC≌△BDF(HL),
∴BF=AC;
∵△ADC≌△BDF,
∴∠EBC=∠DAC.
又∵∠DAC+∠ACD=90°,
∴∠EBC+∠ACD=90°.
∴BE⊥AC,
即BF⊥AC.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.发现并利用两个直角三角形全等是正确解决本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
12.下列说法错误的是( )
| A. | 投掷一枚均匀的骰子,朝上一面的点数是3的概率是$\frac{1}{3}$ | |
| B. | 不可能事件发生的概率为0 | |
| C. | 买一张彩票中奖是随机事件 | |
| D. | 一个事件发生的概率为1%,这件事件就有可能发生 |
 如图是小强用八块相同的小立方块搭建的一个积木,他从左面看到的形状图是( )
如图是小强用八块相同的小立方块搭建的一个积木,他从左面看到的形状图是( )



 如图示在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:
如图示在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论: 有两棵树,一棵高5米,另一棵高2米,两棵树的距离有4米,一只小鸟从一棵树的树顶端飞到另一棵树的顶端,那么请问:这只小鸟至少要飞了5米.
有两棵树,一棵高5米,另一棵高2米,两棵树的距离有4米,一只小鸟从一棵树的树顶端飞到另一棵树的顶端,那么请问:这只小鸟至少要飞了5米.
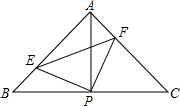 如图,已知△ABC中,AB=AC=2,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC=2,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: