题目内容
9. 有两棵树,一棵高5米,另一棵高2米,两棵树的距离有4米,一只小鸟从一棵树的树顶端飞到另一棵树的顶端,那么请问:这只小鸟至少要飞了5米.
有两棵树,一棵高5米,另一棵高2米,两棵树的距离有4米,一只小鸟从一棵树的树顶端飞到另一棵树的顶端,那么请问:这只小鸟至少要飞了5米.
分析 过点A作AB⊥BC于点B,连接AC,根据勾股定理求出AC的长即可.
解答  解:过点A作AB⊥BC于点B,连接AC,
解:过点A作AB⊥BC于点B,连接AC,
∵一棵高5米,另一棵高2米,两棵树的距离有4米,
∴AB=4m,BC=5-2=3m,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5(m).
故答案为:5.
点评 本题考查的是勾股定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
4.已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,则c的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | 3 | D. | 4 |
14.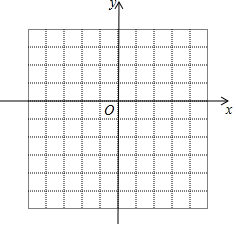 已知二次函数y=-x2-2x+2.
已知二次函数y=-x2-2x+2.
(1)填写表,并在给出的平面直角坐标系中画出这个二次函数的图象;
(2)结合函数图象,直接写出方程-x2-2x+2=0的近似解(指出在哪两个连续整数之间即可).
 已知二次函数y=-x2-2x+2.
已知二次函数y=-x2-2x+2.(1)填写表,并在给出的平面直角坐标系中画出这个二次函数的图象;
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | … |
1.一长方形的一边长为5a-6b,另一边比它小3a-b,则它的周长是( )
| A. | 14a-22b | B. | 14a+22b | C. | 7a+11b | D. | 7a-11b |
19.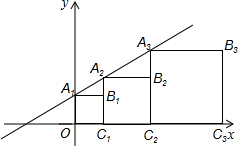 如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
(1)将下列表格补充完整:
(2)写出第4个正方形的边长,并猜想第n个正方形的边长(用含n的代数式表示)
 如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.(1)将下列表格补充完整:
| 坐标 | A1(0,1) | A2(1, 2) | A3( 3, 4) |
| 正方形边长 | A1OC1B1:1 | A2C1C2B2: 2 | A3C2C3B3: 4 |
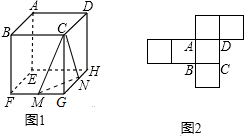 如图,正方体(图1)的展开图如图2所示,在图1中M、N分别是FG、GH的中点,CM、CN、MN是三条线段;请在图2中画出CM、CN、MN这三条线段
如图,正方体(图1)的展开图如图2所示,在图1中M、N分别是FG、GH的中点,CM、CN、MN是三条线段;请在图2中画出CM、CN、MN这三条线段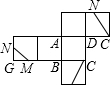 .
. 如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,判断线段BF和AC的数量关系和位置关系,并说明理由.
如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,判断线段BF和AC的数量关系和位置关系,并说明理由.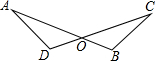 如图,已知AB与CD相交于点O,且AB=CD,当满足OB=OD时,AD=BC.(只需填出一个条件)
如图,已知AB与CD相交于点O,且AB=CD,当满足OB=OD时,AD=BC.(只需填出一个条件)