题目内容
10．
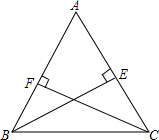如图，在△ABC中，AB=AC．（1）在图上分别画出AB，AC边上的高CF，BE；
（2）S△ABC=$\frac{1}{2}$AC•BE=$\frac{1}{2}$AB•CF；
（3）BE=CF（填“＞”“＜”或“=”）；
（4）由此可以得出结论：等腰三角形两条腰上的高相等．
分析 利用三角形的面积计算公式填空推出结论，总结出结果即可．
解答 解：∵CF，BE是AB，AC边上的高，
∴S△ABC=$\frac{1}{2}$AC•BE=$\frac{1}{2}$AB•CF，
∵AB=AC，
∴BE=CF，
由此可以得出结论：等腰三角形两条腰上的高相等．
故答案为：BE，CF；=，等腰三角形两条腰上的高相等．
点评 此题考查三角形的面积，掌握三角形的面积计算公式是解决问题的关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
20．下列计算正确的是（ ）
| A． | $\root{3}{-8}$=-2 | B． | $\sqrt{36}$=±6 | C． | $\sqrt{3}$$+\sqrt{2}$=$\sqrt{5}$ | D． | $\sqrt{{a}^{2}}$=a |
1．若有三点A、B、C不在同一条直线上，点P满足PA=PB=PC，则平面内这样的点P有（ ）
| A． | 1个 | B． | 2个 | C． | 1个或2个 | D． | 无法确定 |
18．如果把分式$\frac{x+2y}{x+y}$中的x、y的值都变为原来的10倍，那么分式的值（ ）
| A． | 变成原来的10倍 | B． | 缩小为原来的10倍 | ||
| C． | 是原来的$\frac{2}{3}$ | D． | 不变 |
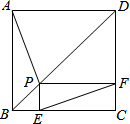如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列四个结论：
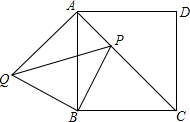如图，在正方形ABCD中，点P是对角线AC上一点，把△BPC绕着点B逆时针旋转得到△BQA．