题目内容
2.当a在什么范围内取值,方程|x2-5x|=x+a有且只有两相异实根?分析 首先分两种情况探讨:x+a>0,x+a<0,得出两个一元二次方程,利用根的判别式建立不等式组,求得答案即可.
解答 解:由题意得:x2-5x=x+a或x2-5x=-(x+a),
x2-6x-a=0或x2-4x+a=0,
△=36+4a或△=16-4a,
因此$\left\{\begin{array}{l}{a>0}\\{36+4a>0}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{16-4a>0}\end{array}\right.$
解得a>0或a<0,
即a≠0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 将下列几何体分类,并说明理由.
将下列几何体分类,并说明理由.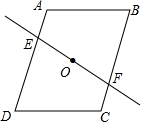 如图,直线EF经过平行四边形ABCD的对角线的交点,若AE=3cm,四边形AEFB的面积为15cm2,则CF=3cm,四边形EDCF的面积为15cm2.
如图,直线EF经过平行四边形ABCD的对角线的交点,若AE=3cm,四边形AEFB的面积为15cm2,则CF=3cm,四边形EDCF的面积为15cm2.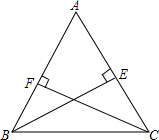 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC. 如图所示是边长为1的正方形网格,点A、B、C、D都在格点上.求图中阴影部分的面积.
如图所示是边长为1的正方形网格,点A、B、C、D都在格点上.求图中阴影部分的面积.