题目内容
7. 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O得切线,与CA的延长线相交于点E,G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O得切线,与CA的延长线相交于点E,G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.(1)求证:BF=EF;
(2)求证:PA是⊙O的切线.
分析 (1)根据切线判定知道EB⊥BC,而AD⊥BC,从而可以确定AD∥BE,那么△BFC∽△DGC,又G是AD的中点,就可得出结论BF=EF.
(2)要证PA是⊙O的切线,就要证明∠PAO=90°,连接AO,AB,根据(1)的结论和BE是⊙O的切线和直角三角形的等量代换,就可得出结论.
解答 解:(1)∵BC是⊙O的直径,BE是⊙O的切线,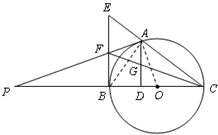
∴EB⊥BC.
又∵AD⊥BC,
∴AD∥BE,
∴△BFC∽△DGC,△FEC∽△GAC,
∴$\frac{BF}{DG}$=$\frac{CF}{CG}$,$\frac{EF}{AG}$=$\frac{CF}{CG}$,
∴$\frac{BF}{DG}$=$\frac{EF}{AG}$,
∵G是AD的中点,
∴DG=AG,
∴BF=EF.
(2)连结AO,AB,
∵BC是⊙O的直径,
∴∠BAC=90°.
在Rt△BAE中,由(1)知F是斜边BE的中点,
∴AF=FB=EF,
∴∠FBA=∠FAB
又∵OA=OB,
∴∠ABO=∠BAO
∵BE是⊙O的切线,
∴∠EBO=90°
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°
∴PA是⊙O的切线.
点评 本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.下列说法正确的是( )
| A. | 射线PA和射线AP是同一条射线 | B. | 射线OA的长度是10cm | ||
| C. | 直线AB、CD相交于点M | D. | 两点确定一条直线 |
18.2008年北京奥运会的比赛门票开始在网上预定,下表为几种球类比赛普通门票价格.小明用490元预定了排球和乒乓球两种门票共8张,求他预定了排球和乒乓球门票各多少张?
| 比赛项目 | 排球 | 篮球 | 足球 | 乒乓球 |
| 票价(元/张) | 50 | 60 | 100 | 80 |
 如图,某测量工作人员与标杆顶端F、电视塔顶端在同一直线上,已知此人眼睛距地面1.5米,标杆为3米,且BC=1米,CD=6米,求电视塔的高ED.
如图,某测量工作人员与标杆顶端F、电视塔顶端在同一直线上,已知此人眼睛距地面1.5米,标杆为3米,且BC=1米,CD=6米,求电视塔的高ED.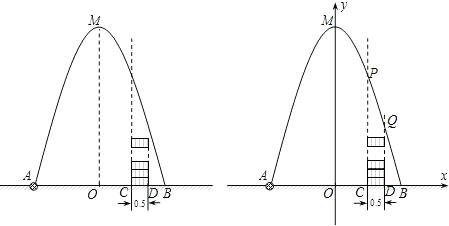
 如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.