题目内容
Rt△ABC中,AC=BC,P为直线AB上一点,以CP为边作正方形CPED,连CE.
(1)如图1,当P为AB的中点,A、E重合时,BP2、AP2、CE2之间的关系是
(2)如图2,当P在AB上运动时,探究BP,AP,CE之间的关系.
(3)如图3,当P在AB的延长线上时,作出图形,并指出②中结论是否成立?(不要求证明)

(1)如图1,当P为AB的中点,A、E重合时,BP2、AP2、CE2之间的关系是
BP2+AP2=CE2
BP2+AP2=CE2
.(2)如图2,当P在AB上运动时,探究BP,AP,CE之间的关系.
(3)如图3,当P在AB的延长线上时,作出图形,并指出②中结论是否成立?(不要求证明)

分析:(1)当P为AB的中点时,先根据直角三角形斜边上的中线等于斜边的一半得出CP=AP=BP=
AB,再由正方形的性质可知∠CPA=90°,根据勾股定理得到CP2+AP2=CE2,即BP2+AP2=CE2;
(2)当P在AB上运动时,连接DA、DP.先利用SAS证明△BCP≌△ACD,根据全等三角形的性质得到BP=AD,∠B=∠CAD,再证明∠DAP=90°,根据勾股定理得出AD2+AP2=PD2,进而得出BP,AP,CE之间的关系为BP2+AP2=CE2;
(3)当P在AB的延长线上时,同(2)可得出BP2+AP2=CE2,即②中结论仍然成立.
| 1 |
| 2 |
(2)当P在AB上运动时,连接DA、DP.先利用SAS证明△BCP≌△ACD,根据全等三角形的性质得到BP=AD,∠B=∠CAD,再证明∠DAP=90°,根据勾股定理得出AD2+AP2=PD2,进而得出BP,AP,CE之间的关系为BP2+AP2=CE2;
(3)当P在AB的延长线上时,同(2)可得出BP2+AP2=CE2,即②中结论仍然成立.
解答:解:(1)如图1,当P为AB的中点,A、E重合时,BP2+AP2=CE2.理由如下:
∵Rt△ABC中,P为AB的中点,
∴CP=AP=BP=
AB.
∵四边形CPED是正方形,
∴∠CPA=90°,
∴CP2+AP2=CE2,
∴BP2+AP2=CE2,
故答案为BP2+AP2=CE2;
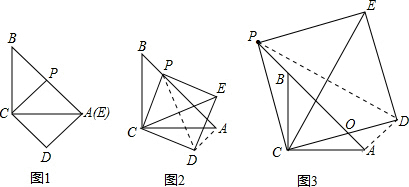 (2)如图2,当P在AB上运动时,BP2+AP2=CE2.理由如下:
(2)如图2,当P在AB上运动时,BP2+AP2=CE2.理由如下:
连接DA、DP.
∵四边形CPED是正方形,
∴CP=CD,PD=CE.
在△BCP与△ACD中,
,
∴△BCP≌△ACD(SAS),
∴BP=AD,∠B=∠CAD,
∵∠B+∠CAB=90°,
∴∠CAD+∠CAB=90°,即∠DAP=90°,
∴AD2+AP2=PD2,
∵AD=BP,PD=CE,
∴BP2+AP2=CE2;
(3)当P在AB的延长线上时,如图3,此时②中结论仍然成立.理由如下:
连接DA、DP,设AP与CD交于点O.
∵四边形CPED是正方形,
∴CP=CD,PD=CE,∠PCD=90°.
在△BCP与△ACD中,
,
∴△BCP≌△ACD(SAS),
∴BP=AD,∠BPC=∠ADC,
∵∠BPC+∠COP=90°,
∴∠ADC+∠DOA=90°,
∴∠DAP=90°,
∴AD2+AP2=PD2,
∵AD=BP,PD=CE,
∴BP2+AP2=CE2.
∵Rt△ABC中,P为AB的中点,
∴CP=AP=BP=
| 1 |
| 2 |
∵四边形CPED是正方形,
∴∠CPA=90°,
∴CP2+AP2=CE2,
∴BP2+AP2=CE2,
故答案为BP2+AP2=CE2;
 (2)如图2,当P在AB上运动时,BP2+AP2=CE2.理由如下:
(2)如图2,当P在AB上运动时,BP2+AP2=CE2.理由如下:连接DA、DP.
∵四边形CPED是正方形,
∴CP=CD,PD=CE.
在△BCP与△ACD中,
|
∴△BCP≌△ACD(SAS),
∴BP=AD,∠B=∠CAD,
∵∠B+∠CAB=90°,
∴∠CAD+∠CAB=90°,即∠DAP=90°,
∴AD2+AP2=PD2,
∵AD=BP,PD=CE,
∴BP2+AP2=CE2;
(3)当P在AB的延长线上时,如图3,此时②中结论仍然成立.理由如下:
连接DA、DP,设AP与CD交于点O.
∵四边形CPED是正方形,
∴CP=CD,PD=CE,∠PCD=90°.
在△BCP与△ACD中,
|
∴△BCP≌△ACD(SAS),
∴BP=AD,∠BPC=∠ADC,
∵∠BPC+∠COP=90°,
∴∠ADC+∠DOA=90°,
∴∠DAP=90°,
∴AD2+AP2=PD2,
∵AD=BP,PD=CE,
∴BP2+AP2=CE2.
点评:本题考查了正方形、直角三角形的性质,全等三角形的判定与性质,勾股定理,综合性较强,难度适中.本题三问,由简单到复杂,层层递进,体现了数学中由特殊到一般的规律.本题通过证明△BCP≌△ACD,得出对应边、对应角相等是解题的关键.

练习册系列答案
相关题目
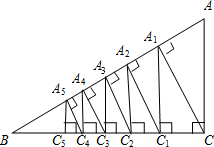 如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,C1A2,…,则CA1=
如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,C1A2,…,则CA1=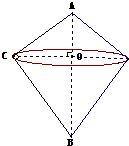 12、如图.在Rt△ABC中,AC=6cm,BC=8cm,以BC 边所在的直线为轴,将△ABC 旋转一周,则所得到的几何体的表面积
12、如图.在Rt△ABC中,AC=6cm,BC=8cm,以BC 边所在的直线为轴,将△ABC 旋转一周,则所得到的几何体的表面积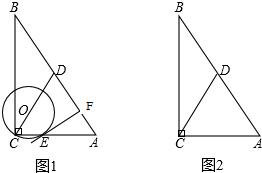 已知:Rt△ABC中,AC⊥BC,CD为AB边上的中线,AC=6cm,BC=8cm;点O是线段CD边上的动点(不与点C、D重合);以点O为圆心、OC为半径的⊙O交AC于点E,EF⊥AB于F.
已知:Rt△ABC中,AC⊥BC,CD为AB边上的中线,AC=6cm,BC=8cm;点O是线段CD边上的动点(不与点C、D重合);以点O为圆心、OC为半径的⊙O交AC于点E,EF⊥AB于F.