题目内容
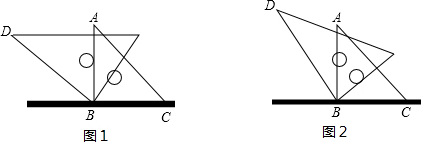
20.将两块三角尺放在桌面上,把直角顶点B重合在一起,如图1,在△ABC中,∠A=∠ACB=45°,在△DEB中,∠D=30°.(1)当DE∥BC时,求∠ABE的度数;
(2)如图2将△ABC按住不动,将三角板DBE绕点B任意旋转(BD、BE均不与桌面重合)时,判断∠ABD与∠CBE有何数量关系?并说明理由;
(3)在(2)的条件下,当三角板DBE绕点B转动时,求∠ABE+∠CBD的值.
分析 (1)在Rt△DBE中,首先求出∠E=60°,再根据平行线的性质求出∠EBC=60°,由此即可解决问题.
(2)结论:∠ABD=∠CBE.由∠ABC=∠DBE,得∠ABD+∠ABE=∠ABE+∠CBE,即可证明.
(3)根据∠CBD+∠ABE=(90°+∠ABD)+∠ABE=90°+(∠ABD+∠ABE),即可证明.
解答 解:(1)如图1中,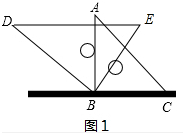
∵在Rt△DBE中,∠DBE=90°,∠D=30°,
∴∠E=60°,
∵DE∥CB,
∴∠E=∠EBC=60°,
∵∠ABC=90°,
∴∠ABE=∠ABC-∠EBC=90°-60°=30°.
(2)如图2中,结论:∠ABD=∠CBE.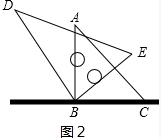
理由:∵∠ABC=∠DBE,
∴∠ABD+∠ABE=∠ABE+∠CBE,
∴∠ABD=∠CBE.
(3)结论:∠ABE+∠CBD=180°.
理由:∵∠CBD=∠ABC+∠ABD=90°+∠ABD,
∴∠CBD+∠ABE=90°+(∠ABD+∠ABE)=90°+90°=180°.
点评 本题考查三角形综合题、平行线的性质,等量代换等知识,解题的关键是熟练应用这些知识解决问题,记住这些基本图形、基本结论,属于中考常考题型.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )
| A. | $\frac{8}{3}$ cm | B. | $\frac{16}{3}$ cm | C. | 3cm | D. | $\frac{4}{3}$ cm |
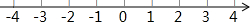 在所给数轴上画出表示数-3,-1$\frac{1}{2}$,|-3$\frac{1}{2}$|,-(-2),0的点,并把这组数从小到大用“<”号连接起来.
在所给数轴上画出表示数-3,-1$\frac{1}{2}$,|-3$\frac{1}{2}$|,-(-2),0的点,并把这组数从小到大用“<”号连接起来.