题目内容
满足(x-3)2+(y-3)2=6的所有实数对(x,y)中,
的最大值是多少?
| y |
| x |
考点:根的判别式
专题:计算题,函数思想
分析:设y=kx,根据直线y=kx与圆(x-3)2+(y-3)2=6相切时k有最大值和最小值,把y=kx代入(x-3)2+(y-3)2=6,得到关于x的一元二次方程,令△=0,得到关于k的一元二次方程,然后解方程,最大解为所求.
解答:解:设y=kx,则直线y=kx与圆(x-3)2+(y-3)2=6相切时k有最大值和最小值,
把y=kx代入(x-3)2+(y-3)2=6,得(1+k2)x2-6(k+1)x+12=0,
∴△=36(k+1)2-4×12×(1+k2)=0,即k2-6k+1=0,
解此方程得,k=3+2
或3-2
.
所以
=k的最大值是3+2
.
把y=kx代入(x-3)2+(y-3)2=6,得(1+k2)x2-6(k+1)x+12=0,
∴△=36(k+1)2-4×12×(1+k2)=0,即k2-6k+1=0,
解此方程得,k=3+2
| 2 |
| 2 |
所以
| y |
| x |
| 2 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了运用△解决函数图象交点的个数问题和一元二次方程的解法.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
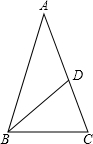 如图,在△ABC中,∠A=36°,AB=AC、BD平分∠ABC.若△ABD的周长比△BCD的周长多1厘米,则BD的长是( )
如图,在△ABC中,∠A=36°,AB=AC、BD平分∠ABC.若△ABD的周长比△BCD的周长多1厘米,则BD的长是( )| A、0.5厘米 | B、1厘米 |
| C、1.5厘米 | D、2厘米 |
在数轴上,坐标是整数的点称为“整点”,设数轴的长度单位是厘米,若在这个数轴上随意画出一条长2008厘米的线段AB,则线段AB盖住的整点至少有( )
| A、2006个 |
| B、2007个 |
| C、2008个 |
| D、2009个 |
已知关于x的方程(m2+2m+3)x=3(x+2)+m-4有唯一解,那么m的值的情况是( )
| A、m=-2 |
| B、m=0 |
| C、m≠-2或m≠0 |
| D、m≠-2且m≠0 |