题目内容
19.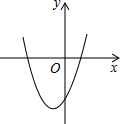 在平面直角坐标系中,二次函数y=x2+2x-3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中-3≤x1<x2≤0,则下列结论正确的是( )
在平面直角坐标系中,二次函数y=x2+2x-3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中-3≤x1<x2≤0,则下列结论正确的是( )| A. | y1<y2 | B. | y1>y2 | C. | y的最小值是-3 | D. | y的最小值是-4 |
分析 根据抛物线解析式求得抛物线的顶点坐标,结合函数图象的增减性进行解答.
解答 解:y=x2+2x-3=(x+3)(x-1),
则该抛物线与x轴的两交点横坐标分别是-3、1.
又y=x2+2x-3=(x+1)2-4,
∴该抛物线的顶点坐标是(-1,-4),对称轴为x=-1.
A、无法确定点A、B离对称轴x=-1的远近,故无法判断y1与y2的大小,故本选项错误;
B、无法确定点A、B离对称轴x=-1的远近,故无法判断y1与y2的大小,故本选项错误;
C、y的最小值是-4,故本选项错误;
D、y的最小值是-4,故本选项正确.
故选:D.
点评 本题考查了二次函数图象上点的坐标特征,二次函数的最值,解题时,利用了“数形结合”的数学思想.

练习册系列答案
相关题目
7. 如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
 如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )| A. | 42° | B. | 48° | C. | 52° | D. | 58° |
14. 如图,直线a∥b,c是截线,∠1的度数是( )
如图,直线a∥b,c是截线,∠1的度数是( )
 如图,直线a∥b,c是截线,∠1的度数是( )
如图,直线a∥b,c是截线,∠1的度数是( )| A. | 55° | B. | 75° | C. | 110° | D. | 125° |
4.一元二次方程x2-4x+4=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
1.某书店把一本新书按标价的八折出售,仍获利20%,若该书进价为20元,则标价( )
| A. | 24元 | B. | 26元 | C. | 28元 | D. | 30元 |
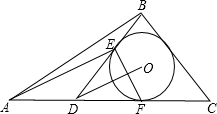 在ABC中,边AC上有一点D满足DC=2AD,O是△BDC的内心,E、F分别为⊙O与边BD、DC的切点,设BD=BC.
在ABC中,边AC上有一点D满足DC=2AD,O是△BDC的内心,E、F分别为⊙O与边BD、DC的切点,设BD=BC.