题目内容
 已知:D为
已知:D为 |
| AC |
(1)求证:AC•BC=2BD•CD;
(2)若AE=3,CD=2
| 5 |
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)如图,作辅助线;证明CF=2CD;证明△BDC∽△CAF,得到
=
,根据CF=2CD,即可解决问题.
(2)如图,证明△ACF∽△DCE,列出比例式求出CE=5,此为解题的关键性结论;证明AB:BC=3:5,借助勾股定理即可解决问题.
| BC |
| CF |
| BD |
| AC |
(2)如图,证明△ACF∽△DCE,列出比例式求出CE=5,此为解题的关键性结论;证明AB:BC=3:5,借助勾股定理即可解决问题.
解答: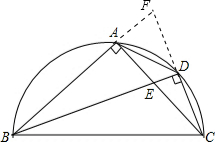 (1)证明:如图,延长CD,交BA的延长线于点F;
(1)证明:如图,延长CD,交BA的延长线于点F;
∵D为
中点,
∴
=
,AD=CD,∠ACD=∠DAC;
∵BC为直径,
∴∠FAC=∠BDC=90°,
∴∠DAF=∠F,AD=DF;
∴CD=DF,CF=2CD;
∵∠FAD=∠BCD,
∴∠F=∠BCD;而∠FAC=∠BDC,
∴△BDC∽△CAF,
∴
=
,而CF=2CD,
∴AC•BC=2BD•CD.
(2)解:设CE=λ;则AC=3+λ,CF=2CD=4
;
∵∠CAF=∠EDC,∠ECD=∠DCE,
∴△ACF∽△DCE,
∴
=
,
=
,
整理得:λ2+3λ-40=0,
解得:λ=5或-8(舍去);
∵D为
中点,AB
∴∠ABE=∠CBE,即BE平分∠ABC,
∴
=
=
,设AB=3μ,则BC=5μ;
由勾股定理得:(3μ)2+82=(5μ)2,
解得:μ=2,
∴AB=6,BC=10.
 (1)证明:如图,延长CD,交BA的延长线于点F;
(1)证明:如图,延长CD,交BA的延长线于点F;∵D为
 |
| AC |
∴
 |
| AD |
 |
| DC |
∵BC为直径,
∴∠FAC=∠BDC=90°,
∴∠DAF=∠F,AD=DF;
∴CD=DF,CF=2CD;
∵∠FAD=∠BCD,
∴∠F=∠BCD;而∠FAC=∠BDC,
∴△BDC∽△CAF,
∴
| BC |
| CF |
| BD |
| AC |
∴AC•BC=2BD•CD.
(2)解:设CE=λ;则AC=3+λ,CF=2CD=4
| 5 |
∵∠CAF=∠EDC,∠ECD=∠DCE,
∴△ACF∽△DCE,
∴
| CF |
| CE |
| AC |
| DC |
4
| ||
| λ |
| 3+λ | ||
2
|
整理得:λ2+3λ-40=0,
解得:λ=5或-8(舍去);
∵D为
 |
| AC |
∴∠ABE=∠CBE,即BE平分∠ABC,
∴
| AB |
| BC |
| AE |
| EC |
| 3 |
| 5 |
由勾股定理得:(3μ)2+82=(5μ)2,
解得:μ=2,
∴AB=6,BC=10.
点评:该题主要考查了圆周角定理及其推论、相似三角形的判定及其性质、勾股定理等几何知识点的应用问题;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
2013年11月11日某淘宝卖家卖出两件商品,它们的售价均为120元,其中一件盈利20%,一件亏损20%,在这次买卖中这位卖家( )
| A、不赔不赚 | B、赔了10元 |
| C、赚了10元 | D、赔了50元 |
 将△ABC向下平移5个单位长度.
将△ABC向下平移5个单位长度. 如图,某隧道的截面是一个半径为4.2米的半圆形,一辆高3.6米,宽3米的卡车能通过隧道吗?为什么?
如图,某隧道的截面是一个半径为4.2米的半圆形,一辆高3.6米,宽3米的卡车能通过隧道吗?为什么?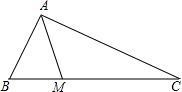 在Rt△ABC中,∠BAC=90°,AB=3,M为边长BC上的点,连接AM,如图,如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是
在Rt△ABC中,∠BAC=90°,AB=3,M为边长BC上的点,连接AM,如图,如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是 如图,BE,CF是△ABC的高,在BE上截取BP=AC,在CF的延长线上截取CQ=AB,求证:AP=AQ,∠QAP=90°.
如图,BE,CF是△ABC的高,在BE上截取BP=AC,在CF的延长线上截取CQ=AB,求证:AP=AQ,∠QAP=90°. 如图,已知△ABC中,D为AC上一点,E为CB延长线上一点,BE=AD,ED和AB相交于点F,求证:EF:FD=AC:BC.
如图,已知△ABC中,D为AC上一点,E为CB延长线上一点,BE=AD,ED和AB相交于点F,求证:EF:FD=AC:BC.