Question

如图，BD是△ABC的角平分线，ED∥BC，交AB于点E．
（1）若∠A=44°，∠BDC=60°，求∠BED的度数；
（2）若∠A-∠ABD=31°，∠EDC=76°，求∠ADB的度数．

Answer 1

考点：平行线的性质,三角形内角和定理,三角形的外角性质

专题：

分析：（1）如图，根据邻补角的定义、△ABD内角和定理以及平行线的性质进行计算；
（2）根据平行线的性质求得∠C=104°；然后利用三角形内角和定理和已知条件易求∠1=∠2=15°．，所以根据三角形外角的性质易求∠ADB的度数．

解答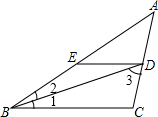：解：如图，∵∠BDC=60°，
∴∠ADB=120°．
又∵∠A=44°，
∴∠2=180°-44°-120°=16°．
∵BD是△ABC的角平分线，
∴∠1=∠2=16°．
又ED∥BC，
∴∠BED+2∠1=180°，
∴∠BED=180°-32°=148°；

（2）∵ED∥BC，
∴∠EDC+∠C=180°．
又∵∠EDC=76°，
∴∠C=104°．
BD是△ABC的角平分线，
∴∠1=∠2．
∵∠A-∠2=31°，∠A+2∠2+∠C=180°
∴∠1=∠2=15°，
∴∠ADB=∠1+∠C=119°．

点评：本题考查了平行线的性质、三角形内角和定理以及三角形外角的性质．此题综合性比较强，需要学生对知识有一系统的掌握．