题目内容
7. 已知,如图,?ABCD中,AE平分∠BAD,交BC于点E,CF平分∠DCB,交AD于点F.求证:△ABE≌△CDF.
已知,如图,?ABCD中,AE平分∠BAD,交BC于点E,CF平分∠DCB,交AD于点F.求证:△ABE≌△CDF.
分析 首先根据平行四边形的性质可得到AB=CD,∠B=∠D,∠BAD=∠DCB,再利用角平分线的性质证明∠BAE=∠DCF,即可得到△ABE≌△CDF的条件,利用ASA即可证明其全等.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,∠BAD=∠DCB,
∵AE平分∠A,CF平分∠C,
∴∠BAE=$\frac{1}{2}$∠BAD,∠DCF=$\frac{1}{2}$∠DCB,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠B=∠D}\\{AB=CD}\\{∠BAE=∠FCD}\end{array}\right.$,
∴△ABE≌△CDF(ASA).
点评 此题主要考查了平行四边形的性质,以及全等三角形的判定,解题的关键是证明∠BAE=∠DCF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列调查中,适合采用抽样调查的是( )
| A. | 调查本班同学的视力 | B. | 调查一批节能灯管的使用寿命 | ||
| C. | 学校招聘教师,对应聘人员面试 | D. | 对乘坐某班客车的乘客进行安检 |
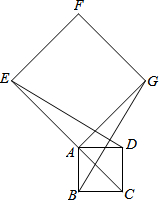 如图,在正方形ABCD中,延长对角线CA到点E,以AE为边作正方形AEFG,连接BG、DE.
如图,在正方形ABCD中,延长对角线CA到点E,以AE为边作正方形AEFG,连接BG、DE.