题目内容
17.解不等式组:-8<$\frac{2-3x}{4}$-6<-5.分析 原式可转化为一个不等式组,先求出两个不等式的解集,再求其公共解.
解答 解:将不等式组化为:$\left\{\begin{array}{l}{-8<\frac{2-3x}{4}-6①}\\{\frac{2-3x}{4}-6<-5②}\end{array}\right.$
由①得x<$\frac{10}{3}$,
由②得x$>-\frac{2}{3}$,
所以不等式组的解集为-$\frac{2}{3}$<x<$\frac{10}{3}$.
点评 此题考查了不等式组的解法;求不等式组的解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
5.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 一次函数图象 | D. | 反比例函数图象 |
9.已知点P(1,2),则P点所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 已知,如图,?ABCD中,AE平分∠BAD,交BC于点E,CF平分∠DCB,交AD于点F.求证:△ABE≌△CDF.
已知,如图,?ABCD中,AE平分∠BAD,交BC于点E,CF平分∠DCB,交AD于点F.求证:△ABE≌△CDF. 实数a、b、c在数轴上的位置如图:则化简$\sqrt{(a-c)^{2}}$-|a+b|的结果是c+b.
实数a、b、c在数轴上的位置如图:则化简$\sqrt{(a-c)^{2}}$-|a+b|的结果是c+b.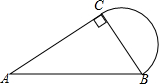 如图,在Rt△ABC中,AC=5cm,AB=7cm,以BC为直径画半圆,求半圆的面积.
如图,在Rt△ABC中,AC=5cm,AB=7cm,以BC为直径画半圆,求半圆的面积.