题目内容
已知一次函数y=
x+m和y=-
x+n的图象都经过点A(-2,0),且与y轴分别交B,C两点,求△ABC的面积和B、C点的坐标.
| 3 |
| 2 |
| 1 |
| 2 |
考点:两条直线相交或平行问题
专题:计算题
分析:先把A点坐标分别代入y=
x+m和y=-
x+n可求出m、n的值,再根据y轴上点的坐标特征求B点和C点坐标,然后根据三角形面积公式计算△ABC的面积.
| 3 |
| 2 |
| 1 |
| 2 |
解答:解:把A(-2,0)代入y=
x+m得
×(-2)+m=0,解得m=3;
把A(-2,0)代入y=-
x+n得-
×(-2)+n=0,解得n=-1,
所以两个一次函数解析式为y=
x+3和y=-
x-1,
当x=0时,y=
x+3=3,则B点坐标为(0,3);当x=0时,y=-
x-1=-1,则C点坐标为(0,-1),
所以△ABC的面积=
×(3+1)×2=4.
| 3 |
| 2 |
| 3 |
| 2 |
把A(-2,0)代入y=-
| 1 |
| 2 |
| 1 |
| 2 |
所以两个一次函数解析式为y=
| 3 |
| 2 |
| 1 |
| 2 |
当x=0时,y=
| 3 |
| 2 |
| 1 |
| 2 |
所以△ABC的面积=
| 1 |
| 2 |
点评:本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
下列说法错误的是( )
| A、斜边和一直角边分别相等的两个直角三角形全等 |
| B、直角三角形两锐角互余 |
| C、两边及一边的对角分别相等的两个三角形全等 |
| D、等角的余角相等 |
若a<b,则下列各式不成立的是( )
| A、ac<bc | ||||
B、
| ||||
| C、a+c<b+c | ||||
| D、a-c<b-c |
 画出下面物体的正投影(正三棱柱)
画出下面物体的正投影(正三棱柱)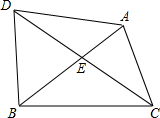 四边形ADBC中,∠ADB=∠ACB,CD平分∠ACB交AB于点E,且BE=CE.若BC=6,AC=4,则BD=
四边形ADBC中,∠ADB=∠ACB,CD平分∠ACB交AB于点E,且BE=CE.若BC=6,AC=4,则BD= 已知,如图,在△ABC中,AB=AC,将△ABC绕点A按顺时方向旋转得△AB1C1,AC1交BB1于点D,DA=DB1,求证:BB1∥AC.
已知,如图,在△ABC中,AB=AC,将△ABC绕点A按顺时方向旋转得△AB1C1,AC1交BB1于点D,DA=DB1,求证:BB1∥AC.