题目内容
3.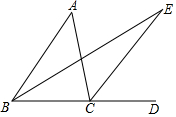 如图,CD是△ABC的边BC的延长线,射线BE、CE相交于点E.
如图,CD是△ABC的边BC的延长线,射线BE、CE相交于点E.(1)若BE、CE分别平分∠ABC、∠ACD,求证:∠E=$\frac{1}{2}∠A$;(提示:∠E=∠ECD-∠EBC)
(2)根据(1)的结论及提示猜想:若∠EBC=$\frac{1}{n}∠ABC$,∠ECD=$\frac{1}{n}∠ACD$,∠A=60°,则∠E的度数为$\frac{60°}{n}$(用含n的式子表示)
(3)在(2)的条件下,当CE∥AB,∠ABC=30°时,求n的值.
分析 (1)根据外角的性质,可得∠A=∠ACD-∠ABC,根据角平分线的定义,可得∠ECD=$\frac{1}{2}$∠ACD,∠EBC=$\frac{1}{2}$∠ABC,再根据∠ECD是△BCE的外角,可得∠E=∠ECD-∠EBC,据此可得结论;
(2)根据外角的性质,可得∠A=∠ACD-∠ABC,根据∠ECD是△BCE的外角,可得∠E=∠ECD-∠EBC,据此可得∠E的度数;
(3)根据平行线的性质,即可得到∠ECD=∠ABC=30°,∠ACE=∠A=60°,根据∠ACD=60°+30°=90°,即可得出∠ECD=$\frac{1}{3}$∠ACD,进而得到n的值.
解答 解:(1)∵∠ACD是△ABC的外角,
∴∠A=∠ACD-∠ABC,
∵BE、CE分别平分∠ABC、∠ACD,
∴∠ECD=$\frac{1}{2}$∠ACD,∠EBC=$\frac{1}{2}$∠ABC,
∵∠ECD是△BCE的外角,
∴∠E=∠ECD-∠EBC=$\frac{1}{2}$∠ACD-$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}∠A$;
(2)∵∠ACD是△ABC的外角,
∴∠A=∠ACD-∠ABC,
∵∠ECD是△BCE的外角,
∴∠E=∠ECD-∠EBC=$\frac{1}{n}∠ACD$-$\frac{1}{n}∠ABC$=$\frac{1}{n}$(∠ACD-∠ABC)=$\frac{1}{n}$∠A=$\frac{60°}{n}$,
故答案为:$\frac{60°}{n}$;
(3)当CE∥AB,∠A=60°,∠ABC=30°时,∠ECD=∠ABC=30°,∠ACE=∠A=60°,
∴∠ACD=60°+30°=90°,
∴∠ECD=$\frac{1}{3}$∠ACD,
∴n=3.
点评 本题主要考查了三角形内角和定理,平行线的性质以及三角形外角的性质的运用,解题时注意:三角形的外角等于与它不相邻的两个内角的和.解决问题的关键是运用三角形外角性质进行计算.

 名校课堂系列答案
名校课堂系列答案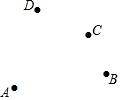 如图,平面上有A、B、C、D四个点,根据下列语句画图.
如图,平面上有A、B、C、D四个点,根据下列语句画图.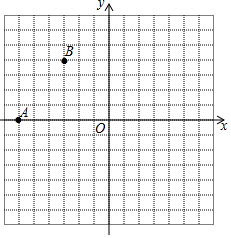 如图,在直角坐标平面内,已知点A的坐标(-6,0).
如图,在直角坐标平面内,已知点A的坐标(-6,0).