题目内容
图①所示的正方体木块棱长为6cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为__________cm.

(3 +3
+3 )cm.
)cm.

【考点】平面展开-最短路径问题;截一个几何体.
【专题】压轴题;数形结合.
【分析】要求蚂蚁爬行的最短距离,需将图②的几何体表面展开,进而根据“两点之间线段最短”得出结果.
【解答】解:如图所示:

△BCD是等腰直角三角形,△ACD是等边三角形,
在Rt△BCD中,CD= =6
=6 cm,
cm,
∴BE= CD=3
CD=3 cm,
cm,
在Rt△ACE中,AE= =3
=3 cm,
cm,
∴从顶点A爬行到顶点B的最短距离为(3 +3
+3 )cm.
)cm.
故答案为:(3 +3
+3 ).
).
【点评】考查了平面展开﹣最短路径问题,本题就是把图②的几何体表面展开成平面图形,根据等腰直角三角形的性质和等边三角形的性质解决问题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.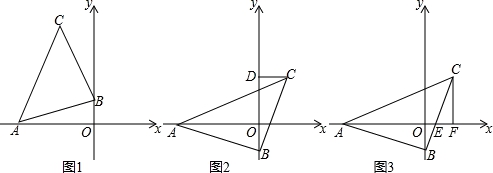
 ,3 D.2,3,4
,3 D.2,3,4 ﹣3
﹣3 +
+ .
. B.
B. C.
C. D.
D.