Question

．如图，一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为(     )

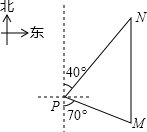
A．40海里    B．60海里    C．70海里    D．80海里

Answer 1

D【考点】等腰三角形的判定与性质；方向角；平行线的性质．

【专题】应用题．

【分析】根据方向角的定义即可求得∠M=70°，∠N=40°，则在△MNP中利用内角和定理求得∠NPM的度数，证明三角形MNP是等腰三角形，即可求解．

【解答】解：MN=2×40=80（海里），

∵∠M=70°，∠N=40°，

∴∠NPM=180°﹣∠M﹣∠N=180°﹣70°﹣40°=70°，

∴∠NPM=∠M，

∴NP=MN=80（海里）．

故选：D．

【点评】本题考查了方向角的定义，以及三角形内角和定理，等腰三角形的判定定理，理解方向角的定义是关键．