题目内容
已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:
(1)∠AEC=∠BED;
(2)AC=BD.

【考点】全等三角形的判定与性质.
【专题】证明题.
【分析】(1)根据CE=DE得出∠ECD=∠EDC,再利用平行线的性质进行证明即可;
(2)根据SAS证明△AEC与△BED全等,再利用全等三角形的性质证明即可.
【解答】证明:(1)∵AB∥CD,
∴∠AEC=∠ECD,∠BED=∠EDC,
∵CE=DE,
∴∠ECD=∠EDC,
∴∠AEC=∠BED;
(2)∵E是AB的中点,
∴AE=BE,
在△AEC和△BED中,
 ,
,
∴△AEC≌△BED(SAS),
∴AC=BD.
【点评】本题主要考查了全等三角形的判定以及全等三角形的性质,关键是根据SAS证明全等.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 B.
B. C.
C. D.
D.

 AB长为半径作弧,两弧交于点C.若点C的坐标为(m﹣1,2n),则m与n的关系为( )
AB长为半径作弧,两弧交于点C.若点C的坐标为(m﹣1,2n),则m与n的关系为( )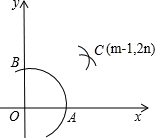

 B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.

