题目内容
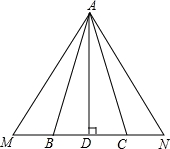
已知,△ABC 是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.
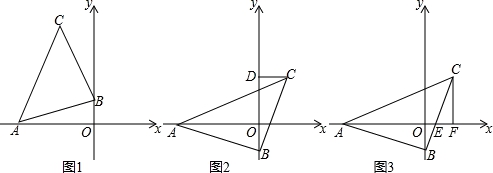
(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,﹣1),求点C的坐标;
(2)如图2,过点C作CD⊥y轴于D,请直接写出线段OA、OD、CD之间等量关系;
(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于F,问CF与AE有怎样的数量关系?并说明理由.
【考点】全等三角形的判定与性质;坐标与图形性质;等腰直角三角形.
【分析】(1)如图1,过点C作CD⊥y轴,CE⊥x轴,则四边形CDOE为矩形,证明△ABO≌△BCD,得到BO=CD=1,OA=DB=3,即可确定C的坐标;
(2)OA=OD+CD;证明△ABO≌△BCD,得到BO=CD,OA=DB,即可解答;
(3)AE=2CF,如图3,延长CF,AB相交于G,证明△AFC≌△AFG,得到CF=GF,再证明△ABE≌△CBG,得到AE=CG,即可解答.
【解答】解:(1)如图1,过点C作CD⊥y轴,CE⊥x轴,则四边形CDOE为矩形,
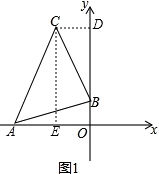
∵A的坐标是(﹣3,0),点B的坐标是(0,﹣1),
∴OA=3,OB=1,
∵CD⊥y轴,
∴∠CDB=90°,∠DCB+∠CBD=90°,
∵∠ABC=90°,
∴∠ABO+∠CBD=90°,
∴∠ABO=∠DCB,
在△ABO和△BCD中,

∴△ABO≌△BCD,
∴BO=CD=1,OA=DB=3,
∴DO=BO+BD=4,EO=CD=1
∴C(﹣1,4);
(2)OA=OD+CD;
∵CD⊥y轴,
∴∠CDB=90°,∠DCB+∠CBD=90°,
∵∠ABC=90°,
∴∠ABO+∠CBD=90°,
∴∠ABO=∠DCB,
在△ABO和△BCD中,

∴△ABO≌△BCD,
∴BO=CD,OA=DB,
∵BD=OB+OD,
 ∴OA=CD+OD.
∴OA=CD+OD.
(3)AE=2CF,
如图3,延长CF,AB相交于G,

证明CF=FG,△ABE≌△CBG.
∵x轴恰好平分∠BAC,
∴∠CAF=∠GAF,
∵CF⊥x轴,
∴∠AFE=∠AFG=90°,
在△AFC和△AFG中,
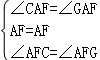
∴△AFC≌△AFG,
∴CF=GF,
∵∠AEB=∠CEF,∠ABE=∠CFE=90°,
∴∠BAE=∠BCG,
在△ABE和△CBG中,

∴△ABE≌△CBG,
∴AE=CG,
∴AE=CF+GF=2CF.
【点评】本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明三角形全等,并利用全等三角形的性质得到相等的线段.

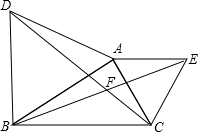
 中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:
中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:

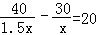 B.
B.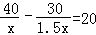
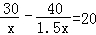 D.
D.
 =__________.
=__________. B.
B. C.
C. D.
D.
