题目内容
5．
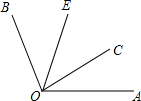如图，已知OC是∠AOB内部的一条射线，∠AOC=30°，OE是∠COB的平分线．当∠BOE=40°时，∠AOB的度数是（ ）| A． | 70° | B． | 80° | C． | 100° | D． | 110° |
分析 根据OE是∠COB的角平分线，则可求得∠COB的度数，然后根据∠AOB=∠AOC+∠COB即可求解．
解答 解：∵OE是∠COB的平分线，
∴∠COB=2∠COE （角平分线的定义）．
∵∠BOE=40°，
∴∠COB=80°．
∵∠AOC=30°，
∴∠AOB=∠AOC+∠COB=110°，
故选D．
点评 本题考查了角度的计算，角度的计算转化为角度的和或差，理解角平分线的定义是关键．
练习册系列答案
相关题目
15．已知α、β均为锐角，且满足|sinα-$\frac{1}{2}$|+$\sqrt{（tanβ-1）^{2}}$=0，则α+β=（ ）
| A． | 60° | B． | 75° | C． | 90° | D． | 105° |
16．若P在第二象限，且到x轴的距离为3，到y轴的距离为6，则点P的坐标为（ ）
| A． | （3，6） | B． | （-3，6） | C． | （-6，3） | D． | （6，3） |
10．已知线段AB=8cm，点C是直线AB上一点，BC=2cm，若M是AB的中点，N是BC的中点，则线段MN的长度为
（ ）
（ ）
| A． | 5cm | B． | 5cm或3cm | C． | 7cm或3cm | D． | 7cm |
17．汽车向南行驶10千米记作10千米，那么汽车向北行驶10千米记作（ ）
| A． | 0千米 | B． | -10千米 | C． | -20千米 | D． | 10千米 |
14．矩形具有而一般平行四边形不具有的特征是（ ）
| A． | 对边相等 | B． | 对角相等 | C． | 对角线相等 | D． | 对角线互相平分 |
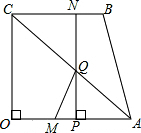如图，四边形OABC为直角梯形，OA∥BC，∠AOC=90°，OA=OC=4，BC=3．点M从O出发以每秒2个单位长度的速度向A运动；点N从B同时出发，以每秒1个单位长度的速度向C运动，当其中一个动点达到终点时，另一个动点也随之停止运动，过点N作NP垂直OA于点P，连接AC交NP于点Q，连接MQ．