题目内容
某同学遇到这样一个问题:已知在△ABC中,AB,BC,AC三边的长分别为
、
、
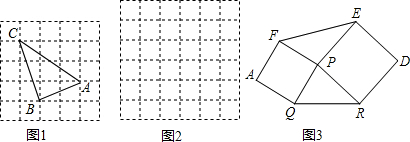
,求△ABC的面积.他是这样解决问题的:如图1,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处).从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.请回答:
(1)图1中△ABC的面积为 ;
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).利用构图法在图2中画出三边长分别为
、2
、
的格点△DEF;
(3)如图3,已知△PQR,以PQ、PR为边向外作正方形PQAF、PRDE,连EF.若PQ=2
,PR=
,QR=
.则六边形AQRDEF的面积为 .
| 5 |
| 10 |
| 13 |
(1)图1中△ABC的面积为
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).利用构图法在图2中画出三边长分别为
| 13 |
| 5 |
| 29 |
(3)如图3,已知△PQR,以PQ、PR为边向外作正方形PQAF、PRDE,连EF.若PQ=2
| 2 |
| 13 |
| 17 |

考点:勾股定理
专题:作图题
分析:(1)利用网格表示出各部分面积,进而得出答案;
(2)利用勾股定理借助网格求出即可;
(3)六边形AQRDEF的面积=边长为2
的正方形面积+边长为
的正方形面积+△PEF的面积+△PQR的面积,其中两个三角形的面积分别用长方形的面积减去各个小三角形的面积.
(2)利用勾股定理借助网格求出即可;
(3)六边形AQRDEF的面积=边长为2
| 2 |
| 13 |
解答:解:(1)△ABC的面积为:3×3-
×2×3-
×1×2-
×1×3=3.5;
故答案为:3.5;
(2)如图所示:
 ;
;
(3)如图:∵S△PEF=5×2-
×2×2-
×2×3=5,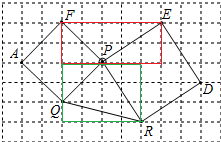
S△PQR=4×3-
×4×1-
×2×2-
×2×3=5,
∴六边形AQRDEF的面积=8+13+5+5=31.
故六边形AQRDEF的面积为31.
故答案为:31.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:3.5;
(2)如图所示:
 ;
;(3)如图:∵S△PEF=5×2-
| 1 |
| 2 |
| 1 |
| 2 |

S△PQR=4×3-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴六边形AQRDEF的面积=8+13+5+5=31.
故六边形AQRDEF的面积为31.
故答案为:31.
点评:此题主要考查了勾股定理以及三角形面积求法,利用勾股定理求出各边长是解题关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知二次函数y=2x2+x+m的图象与x轴有唯一交点,则当-1≤x≤0时,y的取值范围是( )
A、0≤y≤
| ||
B、-
| ||
C、0<y<
| ||
D、-
|
轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同.已知水流的速度是3千米/时,求轮船在静水中的速度.设轮船在静水中的速度为x千米/时,由题意列出方程,其中正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法正确的是( )
| A、有理数都有倒数 |
| B、-x一定是负数 |
| C、两个负数,绝对值大的反而小 |
| D、两个有理数的和一定大于加数 |
 已知△ABC和△ADE中,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,M为中点,连接DM,BM.求证:
已知△ABC和△ADE中,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,M为中点,连接DM,BM.求证: 如图,在△ABC中,∠BAC=40°,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数为
如图,在△ABC中,∠BAC=40°,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数为
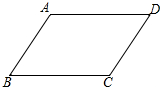 已知AD∥BC,∠A=∠C,问AB∥CD吗?为什么?
已知AD∥BC,∠A=∠C,问AB∥CD吗?为什么?