题目内容
2.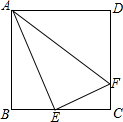 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论:
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论:①∠BAE=30°,②△ABE∽△ECF,③AE⊥EF,④AE=2EF,⑤△ABE∽△AEF.
其中正确结论的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先由线段的关系得出$\frac{AB}{BE}$=$\frac{CE}{CF}$=2,即可判断出①错误,再利用两边对应成比例,夹角相等得出△ABE∽△ECF,△ABE∽△AEF,最后用同角的余角相等,即可得出②③④⑤正确.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠C=∠D=90°
∵E是BC的中点,
∴AE=CE=$\frac{1}{2}$BC=$\frac{1}{2}$AB,
在Rt△ABE中,tan∠BAE=$\frac{BE}{AB}$=$\frac{1}{2}$<$\frac{\sqrt{3}}{3}$,
∵tan30°=$\frac{\sqrt{3}}{3}$,
∴∠BAE<30°,
所以①错误;
∴$\frac{AB}{BE}$=2
∵CD=4CF ,
,
∴$\frac{CE}{CF}$=2,
∴$\frac{AB}{BE}$=$\frac{CE}{CF}$,
∵∠B=∠C,
∴△ABE∽△ECF,
∴$\frac{AE}{EF}=\frac{AB}{CE}$=2,
∴AE=2EF,
所以②④正确;
∵△ABE∽△ECF,
∴∠BAE=∠CEF,
∵∠BAE+∠AEB=90°,
∴∠AEB+∠CEF=90°,
∴∠AEF=90°,
∴AE⊥EF,
所以③正确;
∵$\frac{AB}{BE}$=2,$\frac{AE}{EF}=\frac{AB}{CE}$=2,
∴$\frac{AB}{BE}=\frac{AE}{EF}$,
∵∠B=∠AEF=90°,
∴△ABE∽△AEF,
所以⑤正确,
即:正确的有②③④⑤四个;
故选C.
点评 此题是四边形综合题,主要考查了正方形的性质,相似三角形的性质和判定,锐角三角函数,解本题的关键是判断出△ABE∽△ECF.

练习册系列答案
相关题目
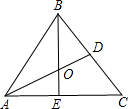 如图,等边三角形的边长为2,中线AD与中线BE相交于点O,则OA2=$\frac{4}{3}$.
如图,等边三角形的边长为2,中线AD与中线BE相交于点O,则OA2=$\frac{4}{3}$.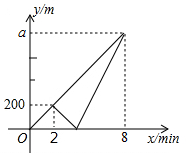 周末,小明和弟弟从家出发,步行去吉林省图书馆学习.出发2分钟后,小明发现弟弟的数学书忘记带了,弟弟继续按原速前往图书馆,小明按原路原速返回家取书,然后骑自行前往图书馆,恰好与弟弟同时到达图书馆.小明和弟弟各自距家的路程y(m)与小明步行的时间x(min)之间的函数图象如图所示.
周末,小明和弟弟从家出发,步行去吉林省图书馆学习.出发2分钟后,小明发现弟弟的数学书忘记带了,弟弟继续按原速前往图书馆,小明按原路原速返回家取书,然后骑自行前往图书馆,恰好与弟弟同时到达图书馆.小明和弟弟各自距家的路程y(m)与小明步行的时间x(min)之间的函数图象如图所示.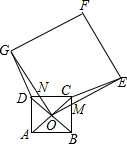 如图,四边形ABCD与四边形OEFG都是正方形,O是正方形ABCD的中心,OE交BC于点M,OG交CD于点N,下列结论:
如图,四边形ABCD与四边形OEFG都是正方形,O是正方形ABCD的中心,OE交BC于点M,OG交CD于点N,下列结论: