题目内容
13.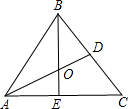 如图,等边三角形的边长为2,中线AD与中线BE相交于点O,则OA2=$\frac{4}{3}$.
如图,等边三角形的边长为2,中线AD与中线BE相交于点O,则OA2=$\frac{4}{3}$.
分析 根据等边三角形三线合一的特点及直角三角形的性质解答即可.
解答 解:∵△ABC是等边三角形,AD、BE为中线;
∴BD=AE=1,∠ABE=∠BAD=30°,∠AEB=∠ADB=90°;
∴AD=BE=AB•sin60°=$\sqrt{3}$;
在Rt△BOD中,BD=1,∠DBO=30°;
∴OD=BD•tan30°=1×$\frac{\sqrt{3}}{3}$;
∴OA=AD-OD=$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
∴OA2的长度$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 此题比较简单,解答此题的关键是熟知等边三角形三线合一的性质.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
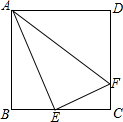 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论:
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论: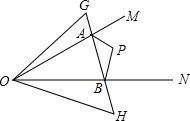 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若∠MON=40°,则∠GOH=80°.
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若∠MON=40°,则∠GOH=80°.