题目内容
14.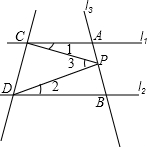 如图,直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
如图,直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.(1)探讨图中∠1、∠2、∠3之间的关系,并说明理由;
(2)如果点P在A、B两点外侧运动时,请直接写出∠1、∠2、∠3之间的关系,不需要说明理由(点P和A、B不重合).
分析 (1)过P作PQ∥l1,根据平行线的性质可求得∠1+∠2=∠3;
(2)当点P在A点外时和在B点外侧时,由平行线的性质和三角形外角的性质可分别得到∠1、∠2、∠3之间的关系.
解答 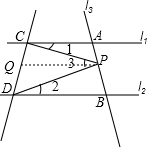 解:(1)∠1+∠2=∠3,理由如下:
解:(1)∠1+∠2=∠3,理由如下:
如图,过P作PQ∥l1,
∵l1∥l2,
∴PQ∥l2,
∴∠1=∠CPQ,∠2=∠DPQ,
∴∠1+∠2=∠3;
(2)如果点P在A点外侧运动时,∠2=∠1+∠3;
如果点P在B点外侧运动时,∠1=∠2+∠3.
点评 本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
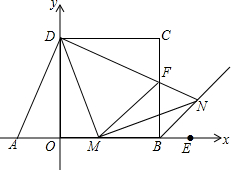 在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O,B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.
在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O,B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N. 在直角△ABC中,∠A=90°,DE⊥BC,BD是∠ABC的平分线,且AC=8,DE=5,求DC的长.
在直角△ABC中,∠A=90°,DE⊥BC,BD是∠ABC的平分线,且AC=8,DE=5,求DC的长.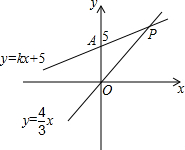 如图,在平面直角坐标系中,一次函数y=kx+5的图象与y轴的交点为点A,与正比例函数y=$\frac{4}{3}$x的图象交于点P.
如图,在平面直角坐标系中,一次函数y=kx+5的图象与y轴的交点为点A,与正比例函数y=$\frac{4}{3}$x的图象交于点P.