ƒøƒ⁄»ð
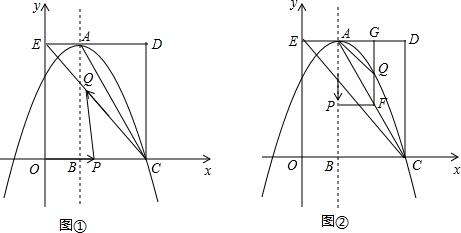
»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨æÿ–ŒOCDEµƒ»˝∏ˆ∂•µ„∑÷± «C£®3£¨0£©£¨D£®3£¨4£©£¨E£®0£¨4£©£Æµ„A‘⁄DE…œ£¨“‘AŒ™∂•µ„µƒ≈◊ŒÔœþπ˝µ„C£¨«“∂‘≥∆÷·x=1Ωªx÷·”⁄µ„B£Æ¡¨Ω”EC£¨AC£Æµ„P£¨QŒ™∂ص„£¨…Ë‘À∂Ø ±º‰Œ™t√ΣÆ
£®1£©ÃÓø’£∫µ„A◊¯±ÍŒ™ £ª≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™ £Æ
£®2£©‘⁄Õº¢Ÿ÷–£¨»Ùµ„P‘⁄œþ∂ŒOC…œ¥”µ„OœÚµ„C“‘1∏ˆµ•Œª/√εƒÀŸ∂»‘À∂Ø£¨Õ¨ ±£¨µ„Q‘⁄œþ∂ŒCE…œ¥”µ„CœÚµ„E“‘2∏ˆµ•Œª/√εƒÀŸ∂»‘À∂Ø£¨µ±“ª∏ˆµ„µΩ¥Ô÷’µ„ ±£¨¡Ì“ª∏ˆµ„ÀÊ÷ÆÕ£÷π‘À∂أƵ±tŒ™∫Œ÷µ ±£¨°˜PCQŒ™÷±Ω«»˝Ω«–Œ£ø
£®3£©‘⁄Õº¢⁄÷–£¨»Ùµ„P‘⁄∂‘≥∆÷·…œ¥”µ„Aø™ ºœÚµ„B“‘1∏ˆµ•Œª/√εƒÀŸ∂»‘À∂Ø£¨π˝µ„P◊ˆPF°ÕAB£¨ΩªAC”⁄µ„F£¨π˝µ„F◊˜FG°ÕAD”⁄µ„G£¨Ωª≈◊ŒÔœþ”⁄µ„Q£¨¡¨Ω”AQ£¨CQ£Æµ±tŒ™∫Œ÷µ ±£¨°˜ACQµƒ√ʪ˝◊Ó¥Û£ø◊Ó¥Û÷µ «∂ý…Ÿ£ø
£®1£©ÃÓø’£∫µ„A◊¯±ÍŒ™
£®2£©‘⁄Õº¢Ÿ÷–£¨»Ùµ„P‘⁄œþ∂ŒOC…œ¥”µ„OœÚµ„C“‘1∏ˆµ•Œª/√εƒÀŸ∂»‘À∂Ø£¨Õ¨ ±£¨µ„Q‘⁄œþ∂ŒCE…œ¥”µ„CœÚµ„E“‘2∏ˆµ•Œª/√εƒÀŸ∂»‘À∂Ø£¨µ±“ª∏ˆµ„µΩ¥Ô÷’µ„ ±£¨¡Ì“ª∏ˆµ„ÀÊ÷ÆÕ£÷π‘À∂أƵ±tŒ™∫Œ÷µ ±£¨°˜PCQŒ™÷±Ω«»˝Ω«–Œ£ø
£®3£©‘⁄Õº¢⁄÷–£¨»Ùµ„P‘⁄∂‘≥∆÷·…œ¥”µ„Aø™ ºœÚµ„B“‘1∏ˆµ•Œª/√εƒÀŸ∂»‘À∂Ø£¨π˝µ„P◊ˆPF°ÕAB£¨ΩªAC”⁄µ„F£¨π˝µ„F◊˜FG°ÕAD”⁄µ„G£¨Ωª≈◊ŒÔœþ”⁄µ„Q£¨¡¨Ω”AQ£¨CQ£Æµ±tŒ™∫Œ÷µ ±£¨°˜ACQµƒ√ʪ˝◊Ó¥Û£ø◊Ó¥Û÷µ «∂ý…Ÿ£ø

øºµ„£∫∂˛¥Œ∫Ø ˝◊€∫œÃ‚,»˝Ω«–Œµƒ√ʪ˝,π¥π…∂®¿Ì,æÿ–Œµƒ–‘÷
◊®Ã‚£∫¥˙ ˝º∏∫Œ◊€∫œÃ‚,—π÷·Ã‚
∑÷Œˆ£∫£®1£©∏˘æð≈◊ŒÔœþµƒ∂‘≥∆÷·”Îæÿ–Œµƒ–‘÷ ø…µ√µ„A◊¯±Í£¨∏˘æð¥˝∂®œµ ˝∑®ø…µ√≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©œ»∏˘æðπ¥π…∂®¿Ìø…µ√CE£¨‘Ÿ∑÷¡Ω÷÷«Èøˆ£∫µ±°œQPC=90°„ ±£ªµ±°œPQC=90°„ ±£ªÃ÷¬€ø…µ√°˜PCQŒ™÷±Ω«»˝Ω«–Œ ±tµƒ÷µ£ª
£®3£©∏˘æð¥˝∂®œµ ˝∑®ø…µ√÷±œþACµƒΩ‚Œˆ Ω£¨∏˘æðS°˜ACQ=S°˜AFQ+S°˜CPQø…µ√S°˜ACQ=-
£®t-2£©2+1£¨“¿¥Àº¥ø…«ÛΩ‚£Æ
£®2£©œ»∏˘æðπ¥π…∂®¿Ìø…µ√CE£¨‘Ÿ∑÷¡Ω÷÷«Èøˆ£∫µ±°œQPC=90°„ ±£ªµ±°œPQC=90°„ ±£ªÃ÷¬€ø…µ√°˜PCQŒ™÷±Ω«»˝Ω«–Œ ±tµƒ÷µ£ª
£®3£©∏˘æð¥˝∂®œµ ˝∑®ø…µ√÷±œþACµƒΩ‚Œˆ Ω£¨∏˘æðS°˜ACQ=S°˜AFQ+S°˜CPQø…µ√S°˜ACQ=-
| 1 |
| 4 |
Ω‚¥£∫Ω‚£∫£®1£©°þ≈◊ŒÔœþµƒ∂‘≥∆÷·Œ™x=1£¨æÿ–ŒOCDEµƒ»˝∏ˆ∂•µ„∑÷± «C£®3£¨0£©£¨D£®3£¨4£©£¨E£®0£¨4£©£¨µ„A‘⁄DE…œ£¨
°ýµ„A◊¯±ÍŒ™£®1£¨4£©£¨
…Ë≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=a£®x-1£©2+4£¨
∞—C£®3£¨0£©¥˙»Î≈◊ŒÔœþµƒΩ‚Œˆ Ω£¨ø…µ√a£®3-1£©2+4=0£¨
Ω‚µ√a=-1£Æ
π ≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=-£®x-1£©2+4£¨º¥y=-x2+2x+3£ª
£®2£©“¿Ã‚“‚”–£∫OC=3£¨OE=4£¨
°ýCE=
=
=5£¨
µ±°œQPC=90°„ ±£¨
°þcos°œQCP=
=
£¨
°ý
=
£¨
Ω‚µ√t=
£ª
µ±°œPQC=90°„ ±£¨
°þcos°œQCP=
=
£¨
°ý
=
£¨
Ω‚µ√t=
£Æ
°ýµ±t=
ªÚt=
±£¨°˜PCQŒ™÷±Ω«»˝Ω«–Œ£ª
£®3£©°þA£®1£¨4£©£¨C£®3£¨0£©£¨
…Ë÷±œþACµƒΩ‚Œˆ ΩŒ™y=kx+b£¨‘Ú
£¨
Ω‚µ√
£Æ
π ÷±œþACµƒΩ‚Œˆ ΩŒ™y=-2x+6£Æ
°þP£®1£¨4-t£©£¨Ω´y=4-t¥˙»Îy=-2x+6÷–£¨µ√x=1+
£¨
°ýQµ„µƒ∫·◊¯±ÍŒ™1+
£¨
Ω´x=1+
¥˙»Îy=-£®x-1£©2+4÷–£¨µ√y=4-
£Æ
°ýQµ„µƒ◊ð◊¯±ÍŒ™4-
£¨
°ýQF=£®4-
£©-£®4-t£©=t-
£¨
°ýS°˜ACQ=S°˜AFQ+S°˜CFQ
=
FQ•AG+
FQ•DG
=
FQ£®AG+DG£©
=
FQ•AD
=
°¡2£®t-
£©
=-
+t
=-
£®t2+4-4t-4£©
=-
£®t-2£©2+1£¨
°ýµ±t=2 ±£¨°˜ACQµƒ√ʪ˝◊Ó¥Û£¨◊Ó¥Û÷µ «1£Æ
°ýµ„A◊¯±ÍŒ™£®1£¨4£©£¨
…Ë≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=a£®x-1£©2+4£¨
∞—C£®3£¨0£©¥˙»Î≈◊ŒÔœþµƒΩ‚Œˆ Ω£¨ø…µ√a£®3-1£©2+4=0£¨
Ω‚µ√a=-1£Æ
π ≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=-£®x-1£©2+4£¨º¥y=-x2+2x+3£ª
£®2£©“¿Ã‚“‚”–£∫OC=3£¨OE=4£¨
°ýCE=
| OC2+OE2 |
| 32+42 |
µ±°œQPC=90°„ ±£¨
°þcos°œQCP=
| PC |
| CQ |
| OC |
| CE |
°ý
| 3-t |
| 2t |
| 3 |
| 5 |
Ω‚µ√t=
| 15 |
| 11 |
µ±°œPQC=90°„ ±£¨
°þcos°œQCP=
| CQ |
| PC |
| OC |
| CE |
°ý
| 2t |
| 3-t |
| 3 |
| 5 |
Ω‚µ√t=
| 9 |
| 13 |
°ýµ±t=
| 15 |
| 11 |
| 9 |
| 13 |
£®3£©°þA£®1£¨4£©£¨C£®3£¨0£©£¨
…Ë÷±œþACµƒΩ‚Œˆ ΩŒ™y=kx+b£¨‘Ú
|
Ω‚µ√
|
π ÷±œþACµƒΩ‚Œˆ ΩŒ™y=-2x+6£Æ
°þP£®1£¨4-t£©£¨Ω´y=4-t¥˙»Îy=-2x+6÷–£¨µ√x=1+
| t |
| 2 |
°ýQµ„µƒ∫·◊¯±ÍŒ™1+
| t |
| 2 |
Ω´x=1+
| t |
| 2 |
| t2 |
| 4 |
°ýQµ„µƒ◊ð◊¯±ÍŒ™4-
| t2 |
| 4 |
°ýQF=£®4-
| t2 |
| 4 |
| t2 |
| 4 |
°ýS°˜ACQ=S°˜AFQ+S°˜CFQ
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| t2 |
| 4 |
=-
| t2 |
| 4 |
=-
| 1 |
| 4 |
=-
| 1 |
| 4 |
°ýµ±t=2 ±£¨°˜ACQµƒ√ʪ˝◊Ó¥Û£¨◊Ó¥Û÷µ «1£Æ
µ„∆¿£∫øº≤È¡À∂˛¥Œ∫Ø ˝◊€∫œÃ‚£¨…ʺ∞µƒ÷™ ∂µ„”–£∫≈◊ŒÔœþµƒ∂‘≥∆÷·£¨æÿ–Œµƒ–‘÷ £¨¥˝∂®œµ ˝∑®«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£¨¥˝∂®œµ ˝∑®«Û÷±œþµƒΩ‚Œˆ Ω£¨π¥π…∂®¿Ì£¨»˝Ω«–Œ√ʪ˝£¨∂˛¥Œ∫Ø ˝µƒ◊Ó÷µ£¨“‘º∞∑÷¿ýÀºœÎµƒ‘À”√£Æ

¡∑œ∞≤·œµ¡–¥∞∏
 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
œýπÿƒø
 »ÁÕº£¨°—Oµƒ∞Îæ∂ «2£¨÷±œþl”ΰ—OœýΩª”⁄A°¢B¡Ωµ„£¨M°¢N «°—O…œµƒ¡Ω∏ˆ∂ص„£¨«“‘⁄÷±œþlµƒ“Ï≤ý£¨»Ù°œAMB=45°„£¨‘ÚÀƒ±þ–ŒMANB√ʪ˝µƒ◊Ó¥Û÷µ «
»ÁÕº£¨°—Oµƒ∞Îæ∂ «2£¨÷±œþl”ΰ—OœýΩª”⁄A°¢B¡Ωµ„£¨M°¢N «°—O…œµƒ¡Ω∏ˆ∂ص„£¨«“‘⁄÷±œþlµƒ“Ï≤ý£¨»Ù°œAMB=45°„£¨‘ÚÀƒ±þ–ŒMANB√ʪ˝µƒ◊Ó¥Û÷µ «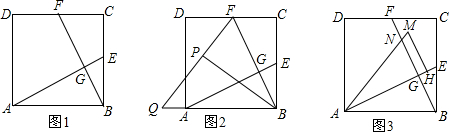
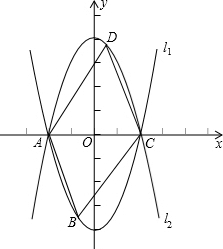 »ÁÕº£¨“—÷™≈◊ŒÔœþl1£∫y=x2-4”Îx÷·œýΩª”⁄A£¨C¡Ωµ„£Æ
»ÁÕº£¨“—÷™≈◊ŒÔœþl1£∫y=x2-4”Îx÷·œýΩª”⁄A£¨C¡Ωµ„£Æ