题目内容

1．已知a，b是方程x2-x-3=0的两个根，则代数式2a3+b2+3a2-11a-b+2000的值为2018．

分析 根据一元二次方程解的定义得到a2-a-3=0，b2-b-3=0，即a2=a+3，b2=b+3，则2a3+b2+3a2-11a-b+2000=2a（a+3）+b+3+3（a+3）-11a-b+2000，整理得2a2-2a+2012，然后再把a2=a+3代入后合并即可．

解答 解：∵a，b是方程x2-x-3=0的两个根，
∴a2-a-3=0，b2-b-3=0，即a2=a+3，b2=b+3，
∴2a3+b2+3a2-11a-b+2000=2a（a+3）+b+3+3（a+3）-11a-b+2000
=2a2-2a+2012
=2（a+3）-2a+2012
=2a+6-2a+2012
=2018．
故答案为：2018．

点评 本题考查了根与系数的关系的知识，解答本题要掌握若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$，也考查了一元二次方程解的定义，此题难度不大．

练习册系列答案
相关题目
11．当x＞$\frac{1}{2}$时，$\sqrt{1-4x+4{x}^{2}}$得2x-1．
12．如图，在菱形ABCD中，对角线AC、BD相交于点O，AB=5，AC=6，过点D作AC的平行线交BC的延长线于点E，
（1）求证：AC=DE；
（2）求△BDE的面积．
9．阅读下面的例题：
解方程x2-|x|-2=0
解：（1）当x≥0，原方程化为x2-x-2=0，解得x1=2，x2=-1（不合题意，舍去）
（2）当x＜0时，原方程化为x2+x-2=0，解得x1=1（不合题意，舍去），x2=-2，∴原方程的根是x1=2，x2=-2
（3）请参照例题解方程x2-|x-1|-2=0．
16．若方程组$\left\{\begin{array}{l}5x-4y=m\\ 3x+5y=8\end{array}\right.$中x与y的值相等，则m的值是（　　）
A．1B．-1C．±1D．±5
6．下列式子中为单项式的有（　　）个
①abc；②$\frac{x+1}{a}$；③$\frac{m}{π}$；④0；⑤$\frac{m+2}{5}$；⑥-t．
A．2B．3C．4D．5
13．（1）设a、b、c为非零有理数，且|a|+a=0，|ab|=ab，|c|-c=0．求代数式|b|-|a+b|-|c-b|+|a-c|的值．
（2）设${（2x-1）^5}={a_5}{x^5}+{a_4}{x^4}+…+{a_1}{x^1}+{a_0}$，求a0+a2+a4的值．
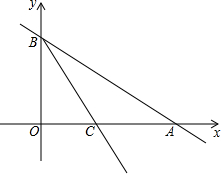10．如图，已知A、B两点是直线AB与x轴的正半轴，y轴的正半轴的交点，如果OA，OB的长分别是x2-14x+48=0的两个根（OA＞OB），射线BC平分∠ABO交x轴于C点，
（1）求OA，OB的长．
（2）求点C的坐标．
（3）在坐标平面内找点Q，使A，B，C，Q四个点为顶点的四边形是平行四边形，求出符合条件的点Q的坐标．
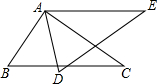11．如图，△ABC≌△ADE，则下列结论成立的是（　　）
①AB=AD，②∠E=∠C，③若∠BAE=120°，∠BAD=40°，则∠BAC=80°，④BC=DE．
A．①B．①②C．①②③D．①②③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网