Question

11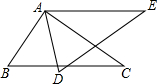．如图，△ABC≌△ADE，则下列结论成立的是（　　）
①AB=AD，②∠E=∠C，③若∠BAE=120°，∠BAD=40°，则∠BAC=80°，④BC=DE．

• A． ①
• B． ①②
• C． ①②③
• D． ①②③④

Answer 1

分析 根据△ABC≌△ADE，可得其对应边对应角相等，即可得AB=AD，∠E=∠C，∠BAC=∠DAE；由∠DAC是公共角易证得∠BAD=∠CAE，已知∠BAE=120°，∠BAD=40°，即可求得∠BAC的度数．

解答 解：∵△ABC≌△ADE，
∴AB=AD，BC=DE，∠E=∠C，∠BAC=∠DAE；
∵∠DAC是公共角
∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE，
已知∠BAE=120°，∠BAD=40°，
∴∠CAE=40°，∠BAC=∠BAE-∠CAE=120°-40°=80°．
故选D．

点评 本题考查了全等三角形的性质及比较角的大小，解题的关键是找到两全等三角形的对应角、对应边．