题目内容
16.计算下列各题:(1)$-\sqrt{3}•\sqrt{(-16)(-36)}$;
(2)(4+$\sqrt{5}$)(4-$\sqrt{5}$);
(3)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$;
(4)$\sqrt{\frac{1}{2}}+\sqrt{\frac{1}{8}}+\sqrt{\frac{1}{32}}$.
分析 (1)根据二次根式的乘法法则运算;
(2)利用平方差公式计算;
(3)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算;
(4)先把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=-$\sqrt{3}$•$\sqrt{16×36}$=-$\sqrt{3}$•$\sqrt{16}$•$\sqrt{36}$=-$\sqrt{3}$•4•6=-24$\sqrt{3}$;
(2)原式=16-5=11;
(3)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$)÷2$\sqrt{3}$
=$\frac{28\sqrt{3}}{3}$÷2$\sqrt{3}$
=$\frac{14}{3}$;
(4)原式=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{2}}{4}$+$\frac{\sqrt{2}}{8}$
=$\frac{7\sqrt{2}}{8}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
4. 如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )
如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )
 如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )
如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
11.已知x+y=7,xy=-8,则x2+y2=( )
| A. | 49 | B. | 65 | C. | 33 | D. | 57 |
8.下列各数中,属于无理数的是( )
| A. | -2 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | 0.101001000 |
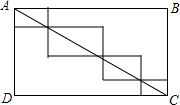 如图,长方形ABCD的边AB=7,BC=4,则图中四个小长方形的周长之和为22.
如图,长方形ABCD的边AB=7,BC=4,则图中四个小长方形的周长之和为22.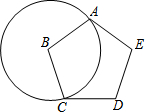 如图所示,正五边形ABCDE的边长为1,⊙B过五边形的顶点A、C,则劣弧AC的长为$\frac{3}{5}$π.
如图所示,正五边形ABCDE的边长为1,⊙B过五边形的顶点A、C,则劣弧AC的长为$\frac{3}{5}$π.