题目内容
9. 如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.
如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.(1)求证:AM=BN;
(2)当MA∥CN时,试求旋转角α的余弦值.
分析 (1)由CA=CB,E,F分别是CA,CB边的三等分点,得CE=CF,根据旋转的性质,CM=CE=CN=CF,∠ACM=∠BCN=α,证明△AMC≌△BNC即可;
(2)当MA∥CN时,∠ACN=∠CAM,由∠ACN+∠ACM=90°,得到∠CAM+∠ACM=90°,所以cosα=$\frac{CM}{AC}$=$\frac{1}{3}$.
解答 解:(1)∵CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,
∴CE=CF ,
,
根据旋转的性质,CM=CE=CN=CF,∠ACM=∠BCN=α,
在△AMC和△BNC中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACM=∠BCN}\\{CM=CN}\end{array}\right.$,
∴△AMC≌△BNC,
∴AM=BN;
(2)∵MA∥CN,
∴∠ACN=∠CAM,
∵∠ACN+∠ACM=90°,
∴∠CAM+∠ACM=90°,
∴∠AMC=90°,
∴cosα=$\frac{CM}{AC}$=$\frac{CE}{AC}$=$\frac{1}{3}$.
点评 本题主要考查了旋转的性质、三角形全等的判定与性质、平行线的性质以及锐角三角函数的综合运用,难度适中,掌握旋转的性质是关键.

练习册系列答案
相关题目
20.化简-16(x-0.5)的结果是( )
| A. | -16x-0.5 | B. | -16x+0.5 | C. | 16x-8 | D. | -16x+8 |
17.某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
| A. | 众数是35 | B. | 中位数是34 | C. | 平均数是35 | D. | 方差是6 |
4.观察下列各式及其展开式:
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
请你猜想(a+b)10的展开式第三项的系数是( )
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
请你猜想(a+b)10的展开式第三项的系数是( )
| A. | 36 | B. | 45 | C. | 55 | D. | 66 |
19.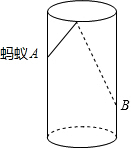 如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
 如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )| A. | 13cm | B. | 2$\sqrt{61}$cm | C. | $\sqrt{61}$cm | D. | 2$\sqrt{34}$cm |
 如图所示是一个等腰三角形纸片ABC,其中AB=AC,把∠B沿EM折叠,使点B落在点D上,把∠C沿FN折叠,使点C也落在点D上.
如图所示是一个等腰三角形纸片ABC,其中AB=AC,把∠B沿EM折叠,使点B落在点D上,把∠C沿FN折叠,使点C也落在点D上. 如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机地向菱形ABCD内掷一粒米,则米粒落到阴影区域内的概率是$\frac{1}{2}$.
如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机地向菱形ABCD内掷一粒米,则米粒落到阴影区域内的概率是$\frac{1}{2}$.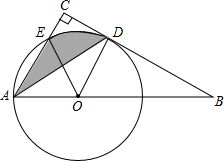 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.