题目内容
19.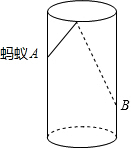 如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )| A. | 13cm | B. | 2$\sqrt{61}$cm | C. | $\sqrt{61}$cm | D. | 2$\sqrt{34}$cm |
分析 将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
解答  解:如图:
解:如图:
∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,
此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,
∴A′D=5cm,BD=12-3+AE=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=$\sqrt{A′{D}^{2}+B{D}^{2}}$
=$\sqrt{{5}^{2}+1{2}^{2}}$
=13(Cm).
故选:A.
点评 本题考查了平面展开---最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.

练习册系列答案
相关题目
14.下列运算结果为a6的是( )
| A. | a2+a3 | B. | a2•a3 | C. | (-a2)3 | D. | a8÷a2 |
 如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.
如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.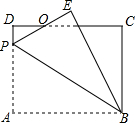 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为4.8.
如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为4.8. 北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7) 把一张矩形纸片按如图所示方式折叠,∠1=30°,则∠2=75°.
把一张矩形纸片按如图所示方式折叠,∠1=30°,则∠2=75°.