题目内容
20.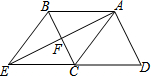 如图,四边形ABCD是平行四边形,点E为DC延长线上一点,联结AE,交BC边于点F,联结BE.
如图,四边形ABCD是平行四边形,点E为DC延长线上一点,联结AE,交BC边于点F,联结BE.(1)求证:AB•AD=BF•ED;
(2)若CD=CA,且∠DAE=90°,求证:四边形ABEC是菱形.
分析 (1)由四边形ABCD是平行四边形得到∠ABC=∠D,AB∥CD,∠BAF=∠DEA,推出△ABF∽△EDA,于是即可得到结论;
(2)根据∠DAE=90°,得到∠AED+∠D=90°,∠EAC+∠DAC=90°,根据CD=CA,推出四边形ABCD是平行四边形,根据平行四边形的性质得到AB∥CD且AB=CD,证出四边形ABEC是平行四边形.由于CE=CA,推出四边形ABEC是菱形.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴∠ABC=∠D,AB∥CD,
∴∠BAF=∠DEA,
∴△ABF∽△EDA,
∴$\frac{AB}{DE}$=$\frac{BF}{AD}$,
∴AB•AD=BF•ED;
(2)∵∠DAE=90°,
∴∠AED+∠D=90°,∠EAC+∠DAC=90°,
∵CD=CA,
∴∠DAC=∠D,
∴∠AED=EAC,
∴CE=CA,
∴CE=CD.
∵四边形ABCD是平行四边形,
∴AB∥CD且AB=CD,
∴AB∥EC且AB=EC,
∴四边形ABEC是平行四边形.
∵CE=CA,
∴四边形ABEC是菱形.
点评 本题考查了平行四边形的判定和性质,相似三角形的判定和性质,菱形的判定,熟记定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.x与6的和一半是非负数,用不等式表示为( )
| A. | $\frac{1}{2}$(x+6)≥0 | B. | $\frac{1}{2}$x+6≤0 | C. | $\frac{1}{2}$x+6≥0 | D. | $\frac{1}{2}$(x+6)≤0 |
5.方程x-$\frac{x-5}{3}$=1,去分母得( )
| A. | 3x-2x+10=1 | B. | x-(x-5)=3 | C. | 3x-(x-5)=3 | D. | 3x-2x+10=6 |
12. 下列四幅图案中,能通过平移左图所示的图案得到的是( )
下列四幅图案中,能通过平移左图所示的图案得到的是( )
 下列四幅图案中,能通过平移左图所示的图案得到的是( )
下列四幅图案中,能通过平移左图所示的图案得到的是( )| A. |  | B. |  | C. |  | D. |  |
10.如果等式(2x-3)x+3=1,则等式成立的x的值的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
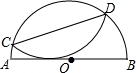 半圆⊙O中,AB为直径,C、D为半圆上任意两点,将$\widehat{CD}$沿直线CD翻折使AB与$\widehat{CD}$相切,已知AB=8,求CD的最大值4$\sqrt{3}$.
半圆⊙O中,AB为直径,C、D为半圆上任意两点,将$\widehat{CD}$沿直线CD翻折使AB与$\widehat{CD}$相切,已知AB=8,求CD的最大值4$\sqrt{3}$.