题目内容
5. 如图,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,且∠BOC=50°,则∠A=80°.
如图,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,且∠BOC=50°,则∠A=80°.
分析 根据三角形的内角和定理求出∠OBC与∠OCB的和,再根据角平分线和平角的定义求出∠DBC与∠ECB的和,又根据三角形内角和求出∠A则可.
解答 解:∵∠ABC和∠ACB的外角平分线交于点O,
∴∠DBC=2∠OBC,∠ECB=2∠OCB,
∵∠BOC=50°,
∴∠OBC+∠OCB=130°,
∴∠DBC+∠ECB=260°,
∴∠A=180°-(∠ABC+∠ACB)
=180°-(180°-∠DBC+180°-∠ECB)
=180°-(360°-260°)
=80°,
故答案为:80°.
点评 本题考查了三角形的内角和定理以及角平分线的性质等知识,解此题的关键是求出∠DBC+∠ECB的度数,涉及范围比较大,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.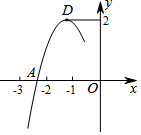 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,其中错误的结论为( )
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,其中错误的结论为( )
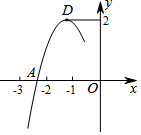 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,其中错误的结论为( )
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,其中错误的结论为( )| A. | 方程ax2+bx+c=0的根为-1 | B. | b2-4ac>0 | ||
| C. | a=c-2 | D. | a+b+c<0 |
17. 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形边长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形边长为( )
 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形边长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形边长为( )| A. | 6 | B. | 5 | C. | $\frac{15}{4}$ | D. | $\sqrt{12}$ |
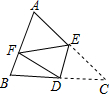 如图,在△ABC中,点D为BC边的中点,点E为AC上一点,将∠C沿DE翻折,使点C落在AB上的点F处,若∠AEF=50°,则∠A的度数为65°.
如图,在△ABC中,点D为BC边的中点,点E为AC上一点,将∠C沿DE翻折,使点C落在AB上的点F处,若∠AEF=50°,则∠A的度数为65°. 如图,⊙O是△ABC的外接圆,OD⊥弦BC,垂足为D,若∠O=50°,则∠A=130°.
如图,⊙O是△ABC的外接圆,OD⊥弦BC,垂足为D,若∠O=50°,则∠A=130°. 如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形,若AB=3,则BC=6.
如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形,若AB=3,则BC=6. 如图,点E、F在AC上,AE=CF,∠AFD=∠CEB,要使△ADF≌△CBE,需要添加的一个条件是∠A=∠C.
如图,点E、F在AC上,AE=CF,∠AFD=∠CEB,要使△ADF≌△CBE,需要添加的一个条件是∠A=∠C.