题目内容
9.解下列一元一次不等式,并把解集表示在数轴上:(1)5(x+2)≥1-2(x-1)
(2)$\frac{23}{7}$-2>2(x+1)
分析 (1)先去括号,再移项、合并同类项,把x的系数化为1即可;
(2)先去分母,再去括号,移项、合并同类项,把x的系数化为1即可.
解答 解:(1)去括号得,5x+10≥1-2x+2,
移项得,5x+2x≥1+2-10,
合并同类项得,7x≥-7,
把x的系数化为1得,x≥-1;
(2)去分母得,23-14>14(x+1),
去括号得,23-14>14x+14,
移项得,-14x>14-23+14,
合并同类项得,-14x>5,
把x的系数化为1得,x<-$\frac{5}{14}$.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
相关题目
20.下列各式计算结果中正确的是( )
| A. | a2+a2=a4 | B. | (-2x2)2=-4x4 | C. | (a+1)2=a2+1 | D. | a•a=a2 |
17.在?ABCD中,对角线AC与BD相交于点O,若AC=8,BD=6,则边长AB的取值范围是( )
| A. | 1<AB<7 | B. | 2<AB<14 | C. | 6<AB<8 | D. | 3<AB<4 |
4.已知等腰三角形的周长为24,腰长为x,则x的取值范围是( )
| A. | x>12 | B. | x<6 | C. | 6<x<12 | D. | 0<x<12 |
14.已知a=255,b=344,c=433,则a、b、c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
18.李老师给出:(a-b)2=5,a2+b2=2,你能计算出ab的值为( )
| A. | -1 | B. | 3 | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |
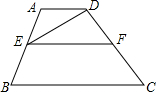 如图,∵∠ADE=∠DEF(已知),
如图,∵∠ADE=∠DEF(已知),