题目内容
19. 如图,64、400分别为所在正方形的面积,则正方形A的面积是( )
如图,64、400分别为所在正方形的面积,则正方形A的面积是( )| A. | 336 | B. | 164094 | C. | 464 | D. | 155904 |
分析 设A的边长为a,根据勾股定理求出a2,得到答案.
解答 解:设A的边长为a,直角三角形斜边的长为c,另乙直角边为b,则c2=400,b2=64,
在直角三角形中,由勾股定理得:a2=c2-b2=400-64=336,
则正方形A的面积是336,
故选:A.
点评 本题考查的是勾股定理的应用,掌握如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
9. 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠ABC=25°,则∠P的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠ABC=25°,则∠P的度数为( )
 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠ABC=25°,则∠P的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠ABC=25°,则∠P的度数为( )| A. | 50° | B. | 40° | C. | 65° | D. | 55° |
4.下列不能用平方差公式计算的是( )
| A. | (-5-a)(a-5) | B. | (-2a+3b)(3b+2a) | C. | (a+b+c)(a-b+c) | D. | (a-b-c)(-a+b+c) |
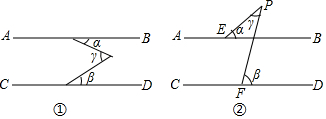
 如图,一个弯形管道ABCD得拐角∠ABC=115°,∠BCD=65°,这时管道所在的直线AB、CD平行吗?写出完整推理说明理由.
如图,一个弯形管道ABCD得拐角∠ABC=115°,∠BCD=65°,这时管道所在的直线AB、CD平行吗?写出完整推理说明理由.