题目内容
12.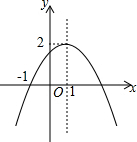 如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:①abc<0;②x=1时,函数的最大值是2;③a+2b+4c>0;④2a=-b;⑤2c>3b.其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:①abc<0;②x=1时,函数的最大值是2;③a+2b+4c>0;④2a=-b;⑤2c>3b.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①对称轴在y轴的右侧,则a、b异号,所以ab<0;
由抛物线与y轴的交点位于y轴的正半轴,则c>0,
所以abc<0,
故①正确;
②∵抛物线的开口方向向下,顶点为(1,2),
∴x=1时,函数的最大值是2,
故②正确;
③x=$\frac{1}{2}$时,y>0,即$\frac{1}{4}$a+$\frac{1}{2}$b+c>0,
∴a+2b+4c>0,
故③正确;
④∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=1,
∴2a=-b,
故④正确;
⑤∵抛物线过点(-1,0),
∴a-b+c=0,
而a=-$\frac{1}{2}$b,
∴-$\frac{1}{2}$b-b+c=0,
∴2c=3b,
故⑤错误.
综上所述,正确的结论有4个.
故选:A.
点评 本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
17.已知线段AB及一点P,如果PA+PB=AB,那么正确的是( )
| A. | P为AB的中点 | B. | P在线段AB上 | C. | P在线段AB外 | D. | P再线段MN上 |
4.合肥市轨道交通1号线隧道工程于今年10月实现全线钻通,项目总投资159.91亿元.“159.91亿”用科学记数法表示正确的是( )
| A. | 159.91×108 | B. | 1.5991×108 | C. | 1.5991×109 | D. | 1.5991×1010 |
1.若∠A=32°12′,∠B=32.12°,∠C=32.2°,则下列结论正确的是( )
| A. | ∠A=∠C | B. | ∠B=∠C | C. | ∠A=∠B | D. | ∠A<∠B |
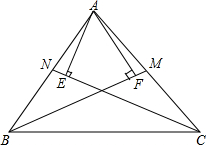 如图,已知AB=AC,BM,CN分别是AC,AB边上的中线,AE⊥CN、AF⊥BM,垂足分别为E,F,求证:AE=AF.
如图,已知AB=AC,BM,CN分别是AC,AB边上的中线,AE⊥CN、AF⊥BM,垂足分别为E,F,求证:AE=AF.