题目内容
2.从甲耻到乙地先下山然后过平路,某人以6千米/时的速度下山,再以4.5千米/时的速度过平路,到达乙地时用了55分钟;返回时以4千米/时的速度过平路,然后以2千米/时的速度上山,到达甲地时用了1$\frac{1}{2}$小时,求甲、乙两地的路程.分析 设从甲地到乙地的下山的路程为x千米,平路的路程为y千米,根据从甲地到达乙地时用了55分钟;从乙地到达甲地时用了1$\frac{1}{2}$小时;列出方程组解答即可.
解答 解:设从甲地到乙地的下山的路程为x千米,平路的路程为y千米,由题意得
$\left\{\begin{array}{l}{\frac{x}{6}+\frac{y}{4.5}=\frac{55}{60}}\\{\frac{x}{2}+\frac{y}{4}=1\frac{1}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1.5}\\{y=3}\end{array}\right.$,
x+y=4.5.
答:甲、乙两地的路程为4.5千米.
点评 此题考查二元一次方程组的实际运用,掌握行程问题中的基本数量关系,得出往返所用的时间和列出方程组解决问题的.

练习册系列答案
相关题目
12.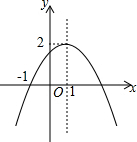 如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:①abc<0;②x=1时,函数的最大值是2;③a+2b+4c>0;④2a=-b;⑤2c>3b.其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:①abc<0;②x=1时,函数的最大值是2;③a+2b+4c>0;④2a=-b;⑤2c>3b.其中正确的结论有( )
 如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:①abc<0;②x=1时,函数的最大值是2;③a+2b+4c>0;④2a=-b;⑤2c>3b.其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:①abc<0;②x=1时,函数的最大值是2;③a+2b+4c>0;④2a=-b;⑤2c>3b.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.在△ABC与△A′B′C′中,已知∠A=∠A′,AC=A′C′,下列说法错误的是( )
| A. | 若添加条件AB=A′B′,则△ABC与△A′B′C′全等 | |
| B. | 若添加条件∠C=∠C′,则△ABC与△A′B′C′全等 | |
| C. | 若添加条件∠B=∠B′,则△ABC与△A′B′C′全等 | |
| D. | 若添加条件BC=B′C′,则△ABC与△A′B′C′全等 |