题目内容
2. 在?ABCD中,点E、F分别在AB、CD上,且AE=CF.求证:DE=BF.
在?ABCD中,点E、F分别在AB、CD上,且AE=CF.求证:DE=BF.
分析 由“平行四边形ABCD的对边平行且相等”的性质推知AB=CD,AB∥CD.然后根据图形中相关线段间的和差关系求得BE=FD,易证四边形EBFD是平行四边形,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∵AE=CF.
∴BE=FD,BE∥FD,
∴四边形EBFD是平行四边形,
∴DE=BF.
点评 本题考查了平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
12.为了解九(3)班学生每天零花钱的使用情况,小明随机调查了20名同学,结果如表:关于这20名同学每天使用的零花钱,下列说法错误的是( )
| 每天使用零花钱(单位:元) | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 2 | 5 | 6 | 4 | 2 | 1 |
| A. | 众数是2元 | B. | 中位数是2元 | C. | 极差是5元 | D. | 平均数是2.45元 |
14.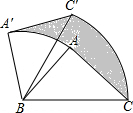 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )
 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )| A. | π | B. | $\frac{3π}{2}$ | C. | $\frac{5π}{2}$ | D. | 3π |
11. 如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )| A. | 遇 | B. | 见 | C. | 未 | D. | 来 |

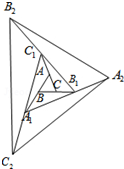 如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.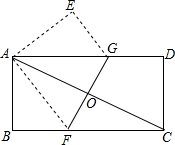 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为6.
如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为6.