题目内容
16.如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD成轴对称的△BC′D.(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且k=-$\frac{\sqrt{3}}{3}$时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作与△DOE成轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
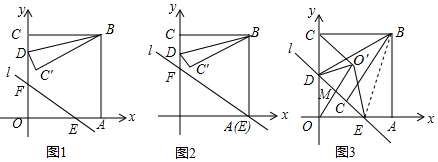
分析 (1)利用翻折变换的性质得出∠CBD=∠C′BD=15°,C′B=CB=2,进而得出CH的长,进而得出答案;
(2)首先求出直线AF的解析式,进而得出当D与O重合时,点C′与A重合,且BC′扫过的图形与△OAF重合部分是弓形,求出即可;
(3)根据题意得出△DO′E与△COO′相似,则△COO′必是Rt△,进而得出Rt△BAE≌Rt△BC′E(HL),再利用勾股定理求出EO的长进而得出答案.
解答  解:(1)∵△CBD≌△C′BD,
解:(1)∵△CBD≌△C′BD,
∴∠CBD=∠C′BD=15°,C′B=CB=2,
∴∠CBC′=30°,
如图1,作C′H⊥BC于H,则C′H=1,HB=$\sqrt{3}$,
∴CH=2-$\sqrt{3}$,
∴点C′的坐标为:(2-$\sqrt{3}$,1);
(2)如图2,∵A(2,0),k=-$\frac{\sqrt{3}}{3}$,
∴代入直线AF的解析式为:y=-$\frac{\sqrt{3}}{3}$x+b,
∴b=$\frac{2\sqrt{3}}{3}$,
则直线AF的解析式为:y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$,
∴∠OAF=30°,∠BAF=60°,故∠BAC′=60°,
∵在点D由C到O的运动过程中,BC′扫过的图形是扇形,
∴当D与O重合时,点C′与A重合,
且BC′扫过的图形与△OAF重合部分是弓形
当C′在直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$上时,BC′=BC=AB,∠BAC′=60°,
∴△ABC′是等边三角形,这时∠ABC′=60°,
∴重叠部分的面积是:$\frac{60π×{2}^{2}}{360}$-$\frac{\sqrt{3}}{4}$×22=$\frac{2}{3}$π-$\sqrt{3}$;
(3)如图3,设OO′与DE交于点M,则O′M=OM,OO′⊥DE,
若△DO′E与△COO′相似,则△COO′必是Rt△,
在点D由C到O的运动过程中,△COO′中显然只能∠CO′O=90°,
∴CO′∥DE,
∴CD=OD=1,
∴b=1,
连接BE,由轴对称性可知C′D=CD,BC′=BC=BA,
∠BC′E=∠BCD=∠BAE=90°,
在Rt△BAE和Rt△BC′E中
∵$\left\{\begin{array}{l}{BE=BE}\\{AB=BC′}\end{array}\right.$,
∴Rt△BAE≌Rt△BC′E(HL),
∴AE=C′E,
∴DE=DC′+C′E=DC+AE,
设OE=x,则AE=2-x,
∴DE=DC+AE=3-x,
由勾股定理得:x2+1=(3-x)2,
解得:x=$\frac{4}{3}$,
∵D(0,1),E($\frac{4}{3}$,0),
∴$\frac{4}{3}$k+1=0,
解得:k=-$\frac{3}{4}$,
∴存在点D,使△DO′E与△COO′相似,这时k=-$\frac{3}{4}$,b=1.
点评 此题主要考查了相似形综合以及全等三角形的判定与性质、勾股定理、待定系数法求一次函数解析式等知识,正确得出AE=C′E是解题关键.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
 如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )| A. | 遇 | B. | 见 | C. | 未 | D. | 来 |

任取一个是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
| A. | $\frac{400}{x}$=$\frac{400+100}{x+20}$ | B. | $\frac{400}{x}$=$\frac{400-100}{x-20}$ | ||
| C. | $\frac{400}{x}$=$\frac{400+100}{x-20}$ | D. | $\frac{400}{x}$=$\frac{400-100}{x+20}$ |
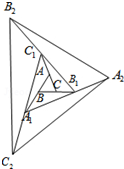 如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).