题目内容
15.已知二元一次方程组$\left\{\begin{array}{l}{x-y=a+3}\\{2x+y=5a}\end{array}\right.$的解集是x<y<0.(1)求字母a的取值范围;
(2)解关于m的不等式am+2<-2m-a.
分析 (1)利用加减消元法解方程组得到x=2a+1和y=a-2,利用x<y<0得到2a+1<a-2<0,然后解关于a的不等式组即可.
(2)把不等式变形(a+2)m<-(a+2),然后利用a的范围确定a+2为负数,然后根据不等式的性质求不等式.
解答 解:(1)$\left\{\begin{array}{l}{x-y=a+3①}\\{2x+y=5a②}\end{array}\right.$,
①+②得3x=6a+3,解得x=2a+1,
把x=2a+1代入②得4a+2+y=5a,解得y=a-2,
∵x<y<0,
∴2a+1<a-2<0,
∴a<-3;
(2)am+2m<-a-2,
(a+2)m<-(a+2),
∵a<-3,
∴m>-1.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
5.用配方法解一元二次方程x2+4x-3=0时,原方程可变形为( )
| A. | (x+2)2=1 | B. | (x+2)2=19 | C. | (x+2)2=13 | D. | (x+2)2=7 |
20.独山县开展关于精准扶贫、精准扶贫的决策部署以来,某贫困户2014年人均纯收入为2620元,经过帮扶到2016年人均纯收入为3850元,设该贫困户每年纯收入的平均增长率为x,则下面列出的方程中正确的是( )
| A. | 2620(1+x)2=3850 | B. | 2620(1+x)=3850 | C. | 2620(1+2x)=3850 | D. | 2620(1+x)2=3850 |
4.杭州1月份连续四天每天的平均气温分别是:1°C、-1°C、0°C、-2°C、则平均气温中最低的是( )
| A. | -1°C | B. | 0°C | C. | 1°C | D. | -2°C |
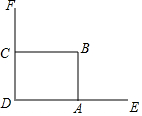 某县扶贫开发办公室为帮助该县贫困户开发经济、发展生产、特为贫困户建设养鸡舍及围栏.在为某农户修建鸡舍时,该农户想借助如图所示的直角旧墙角,用22米长的围栏(全部用完)围成一个矩形鸡舍ABCD,点C在墙DF(墙DF的长为11米)上,点A在墙DE(墙DE足够长)上.(围栏只围AB,BC两边)
某县扶贫开发办公室为帮助该县贫困户开发经济、发展生产、特为贫困户建设养鸡舍及围栏.在为某农户修建鸡舍时,该农户想借助如图所示的直角旧墙角,用22米长的围栏(全部用完)围成一个矩形鸡舍ABCD,点C在墙DF(墙DF的长为11米)上,点A在墙DE(墙DE足够长)上.(围栏只围AB,BC两边)