题目内容
已知一次函数y=（2+m）x-2的函数值y随x的增大而减小，化简|1-|1+m||= ．
考点：一次函数图象与系数的关系
专题：
分析：先根据一次函数的增减性得出关于m的不等式，求出m的取值范围后再计算绝对值．
解答：解：∵一次函数y=（2+m）x-2的函数值y随x的增大而减小，
∴2+m＜0，
解得 m＜-2．
∴m+2＜0，m+1＜-1．
∴|1-|1+m||=|1+1+m|=|2+m|=-2-m．
故答案是：-2-m．
∴2+m＜0，
解得 m＜-2．
∴m+2＜0，m+1＜-1．
∴|1-|1+m||=|1+1+m|=|2+m|=-2-m．
故答案是：-2-m．
点评：本题考查的是一次函数的图象与系数的关系，熟知一次函数y=kx+b（k≠0）中，当k＜0时，y随x的增大而减小是解答此题的关键．
练习册系列答案
相关题目
如图，武汉二中广雅中学为了美化学校环境，准备把学校教学楼对面一栋楼房拐角处的空地利用起来．如图，墙PM⊥PN，PM、PN总长15米，在墙角的外侧用36米长的篱笆围起来种花草．要求：AB⊥MP、DE⊥PN、BC⊥AB、CD⊥DE、AB=DE．设AB=x米，凹六边形ABCDEPA的面积为y平方米．点（2，6）关于x轴对称点坐标为（ ）
| A、（2，-6） |
| B、（-2，-6） |
| C、（-2，6） |
| D、（6，2） |
直线y=3x+9与y轴的交点坐标是（ ）
| A、（0，9） |
| B、（0，9） |
| C、（0，3） |
| D、（3，0） |
棱长为a的正方体，摆放成如图所示的形状．
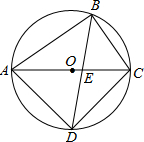已知四边形ABCD内接于⊙O，AC是直径，BD、AC交于点E，AD=DC．